9-BST Implementations of Other ADT functions

BST Implementations of Other ADT Functions

We will consider these implementations - select, join, recursive. Select and Sort is very important and distinguishing feature of BSTs.

To implement select we can use recursive procedure same as quicksort-based selection.

To find the item with kth smallest key in a BST, we check the number of nodes in the left subtree. If there are k nodes there, then we return the item at the root. Otherwise, if more than k nodes, we can recursively search for it. If neither of above condition holds, then the left subtree has t elements with t<k, and $k^{th}$ smallest element in the BST is the k-t-1 st smallest item in the right subtree.

Selection with a BST

private:
	Item selectR(link h, int k)
    {	if(h==0) return nullItem;
    	int t = (h->l==0) ? 0 : h->l->N;
    	if(t>k) reutrn selectR(h->l,k);
    	if(t<k) return selectR(h->r,k-t-1);
    	return h->item;
    }
public:
	Item select(int k)
    { return selectR(head,k);}

Primary reason for including count in a BST is because of implementing the select operation at the cost of memory

We can change this implementation into a partition operation, which rearranges the tree to put the $k^{th}$ smallest element at the root, with precisely the same recursive technique used for root insertion.

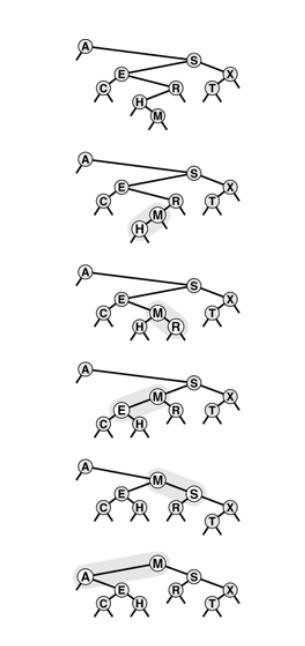
image-20201230085713919

To remove a node with a given key from a BST, we first check whether node is one of the subtree. If it is, we replace result of(recursively) removing the node from it. Now if node is at root, we replace the tree with the result of combining the two subtrees into one tree.

To combine two BSTs with all keys in the second known to be larger than all keys in the first , we apply partition operation on the second tree, to bring smallest element in that tree to the root. At this point, the left subtree of the root must be empty and we can finish job by replacing that link with a link to the first tree.

This approach is asymmetric and is ad hoc in one sense. we could have taken the largest element or left and did a join to the right or many variation of it. All suffer a similar flaw: The tree remaining after removal is not random, even if it was random beforehand.

Root removal in BST

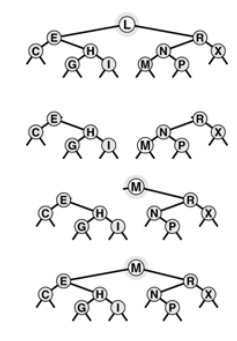
image-20201230085946816

Partitioning of a BST

void partR(link& h, int k)
	{ int t = (h->l == 0) ? 0 : h->l->N;
      if( t > k )
      {partR(h->l,k); rotR(h);}
      if( t < k )
      { partR(h->r, k-t-1); rotL(h);}
    }

Removal is more complicated than search. One easy and lazy approach is to mark them “removed” so that they won’t appear in further search (that is we don’t check for equality with them) or we could periodically rebuild the entire data structure.

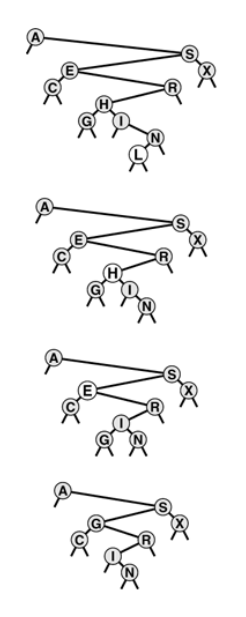
BST node removal

Sequence depicts the result of removing the nodes with keys L, H, E from the BST at the top.

image-20201230090354396

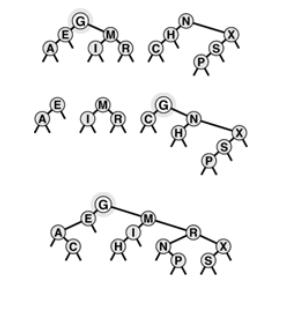
The primary challenge in implementing a function to remove a node with a given handle(link) is the same as it was for linked lists. There are at least 4 ways to address this.

  1. we could add a third link in each tree node, pointing to its parent. ( Problem is that it becomes complex and cumbersome to maintain the extra links)
  2. we could use the key in the item to search in the tree, stopping when we find a matching pointer (disadvantage is that average position of a node is near the bottom of tree so it require unnecessary trips to the bottom of tree)
  3. we could use a reference or a pointer to the pointer to the node as the handle. ( only applicable C/C++0)
  4. Lazy approach to mark them deleted and not listing while searching anymore and periodically rebuilding the data structure.

Removal of a node with a given key in a BST

private:
	link joinLR(link a, link b)
    {
        if(b == 0) return a;
        partR(b,0); b->l = a;
        return b;
    }
	void removeR(link& h, Key v)
    {
        if (h==0) return;
        Key w = h->item.key();
        if(v<w) removeR(h->l,v);
        if(w<v) removeR(h->R,v);
        if(v == w)
        {link t = h;
         h = joinLR(h->l,h->r); delete t;}
    }
public:
	void remove(Item x)
    {removeR(head, x.key());}

Last operation to consider is that join operation i.e. merging two trees. There are many algorithms with their own disadvantages and advantages. for example we could traverse first BST, inserting each of its node into the second BST ( one-liner: use insert into the second BST as a function parameter to a traversal of the first BST ). This is not linear time algorithm. Another approach is to traverse both BST put them in a array to merge them and build a new BST. This can be done in linear time put could potentially require a very large array.

Joining of two BSTs

private:
	link joinR(link a, link b)
    {
        if(b==0) return a;
        if(a==0) return b;
        insertT(b,a->item);
        b->l = joinR(a->l,b->l);
        b->r = joinR(a->r,b->r);
        delete a; return b;
    }
public:
	void join(ST<Item, Key>& b)
    { head = joinR(head, b.head);}

image-20201230093300117

BSTs are widely used for dynamic symbol tables.

Despite their utility, there are two primary drawbacks to BSTs in application.

  1. A substantial amount of space is consumed for links. (i.e. 2/3 rd of memory is used by links and 1/3rd is by data) but it might not be an issue in environments where pointers are large but if memory is at premium we look for other options like hashing.
  2. Poorly Balanced BST could lead to slow performance.