3-Top-Down 2-3-4 Tress
Top-Down 2-3-4 Trees
despite performance guarantees that we get from randomized BSTs and with splay BST but still both admits a possibilities of particular search can take linear time.
Therefore do not help us answer the fundamental question that is : Is there a type of BST in which search and insertion both take logarithmic in the size of tree.
To guarantee that our BSTs will be balanced, we need this flexibility in the tree structures that we use. To get this flexibility, let us assume that the node in our trees can hold more than one key.
Def 1
A 2-3-4 search tree is a tree that either is empty or comprises three types of nodes : 2-nodes, with one key, a left link to a tree with smaller keys, and a right link to a tree with larger keys; 3-nodes, with two keys, a left link to a tree with smaller keys, a middle link to key values in between the node’s keys and a right link to a tree with larger keys; and 4-nodes, with three keys and four links to trees with keys values defined by ranges subtended by the node’s keys.
Def 2
A balanced 2-3-4 search tree is a 2-3-4 search tree with all links to empty trees at the same distance from the root.
here 2-3-4 trees is used in more generalised sense to represent wide variety of trees.
To insert a new node in a 2-3-4 tree, we could do an unsuccessful search and then hook on the node, as we did with BSTs, but tree won’t be balanced anymore. Primary reason that 2-3-4 trees are important is that we can do insertion and still maintain perfect balance in the tree, in every case.
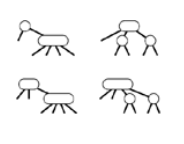
if search ends at 2-node we make it 3-node and if it ends at 3-node we make it 4-nodes but what to do if it ends at the 4-node. We can split 4-nodes into two 2-nodes and send up the middle key to be parent of both 2-nodes.
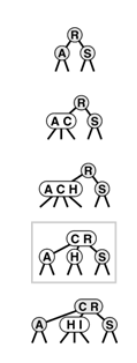
Splitting 4-nodes
Property : Searches in N-node 2-3-4 trees visit at most $\lg N +1$.
Property : Insertion into N-node 2-3-4 trees require fewer than $\lg N +1$ node splits in the worst case, and seen to require less than one node split on the average.
There are many ways to maintain balance in 2-3-4 search trees.
for example : we can balance from the bottom up. First do a search in the tree to find the bottom node where the item to be inserted belongs. If that node is a 2-node or a 3-node, we grow it to a 3-node or a 4-node, just as before. If it is a 4-node, we split it as before (inserting the new item into one of the resulting 2-nodes at the bottom), and insert the middle item into the parent, if the parent is a 2-node or 3-node. If the parent is a 4-node, we split that node ( inserting the middle node from the bottom into the appropriate 2-node), and insert the middle item into its parent, if the parent is a 2-node or a 3-node. If the grandparent is also a 4-node we continue up the tree in the same way, splitting 4-nodes until we encounter a 2-node or 3-node on the search path.