6 Graph Generators
Graph Generators
**Random Edges : **
This model is simple to implement, as indicated by generator given. For given number of vertices $V$, we generate random edges by generating pairs of numbers between $0$ and $V-1$. This is likely to generate random multigraph with self-loops. when removed parallel edges removed we get small amount of edges that’s why its normally used for sparse graph.
17.12 Random graph generator (random edges)
static void randE(Graph &G, int E){
for(int i = 0; i<E; i++)
{
int v = int(G.V()*rand()/(1.0 + RAND_MAX)); int w = int(G.V()*rand()/(1.0 + RAND_MAX));
G.insert(Edge(v,w));
}
}
Random Graph :
Classical Mathematical model for random graphs is to consider all possible edges and to include each in the graph with a fixed probability $p$. If we want the expected number of edges in the graph to be $E$, we can choose $p=2E/V(V-1)$. This implementation is well suited for dense graphs, but not for sparse graphs, since it runs in time proportional to $V(V-1)/2$ to generate just $E=pV(V-1)/2$ edges.
Graphs encountered in practical situations have a property called locality property - edges are much more likely to connect a given vertex to vertices in a particular set than to vertices that are not in the set.
17.13 Random graph generator (random graph)
static void randG(Graph &G, int E){
for(int i = 0; i<E; i++)
{
double p = 2.0*E/G.V() / (G.V()-1);
for(int i = 0 ; i<G.V();i++ )
for(int j = 0 ; j <i ;j++)
if(rand()<p*RAND_MAX)
G.inert(Edge(i,j));
}
}
k-neighbor graph The graph in figure can be generated from simple modification of random-edges graph generator, where we randomly pick the first vertex v, then randomly pick the second from among those whose indices are within a fixed constant k of v (wrapping around from $V-1$ to $0$ ), when the vertices are arranged in a circle.
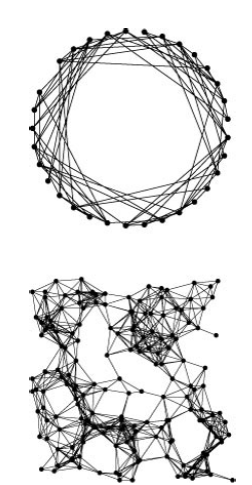
Euclidean Neighbor Graph : (bottom figure)
this graph generates $V$ points in the plane with random co-ordinates between 0 and 1, and then generates edges connecting any two points within distance $d$ of one another.
if $d$ is small, the graph is sparse; if $d$ is large, the graph is dense. There is a possible defect in this model that the graphs are not likely to be connected when they are sparse.
Transaction graph :
Each vertex defined for each phone number, and an edge for each pair $i$ and $j$ with the property that $i$ made a telephone call to $j$ within some fixed period.
This sets of edges represent a huge multigraph. It certainly is sparse, since each person call to a tiny fraction of available telephones.
Program 17.14 Building a graph from pairs of symbols
#include “ST.cc”
template <class Graph>
void IO<Graph>::scan(Graph &G)
{ string v, w;
ST st;
while (cin >> v >> w)
G.insert(Edge(st.index(v), st.index(w)));
}
Function Call Graph :
we can associate a graph with a functions as vertices and an edge connecting $X$ to $Y$ whenever $X$ calls function $Y$. Two different graphs are of interest : the static version, where we create edges at compile time corresponding to the function calls that appear in the program text to each function; and a dynamic version, where we create edges at run time when the calls actually happen. Static Graphs are good to study the program structure while dynamic graphs could give us insights in program behavior.
There are some graphs which are based on implicit connection among items.
- Degrees-of-separation graph
- Interval Graph