8-Generalized Graph Search

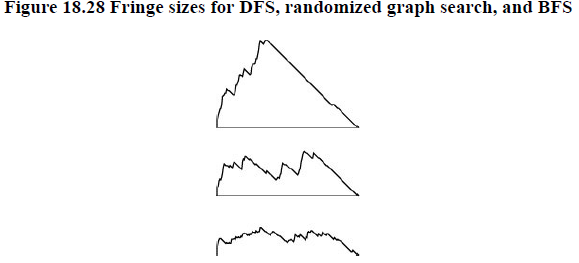
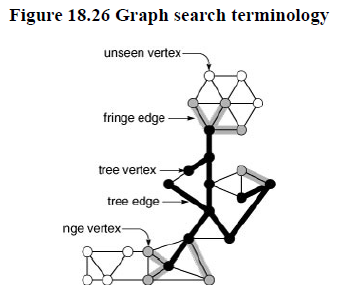
We use term fringe, instead of queue, to describe the set of edges for possible candidates for being next added to the tree.

Starting with a self-loop to a start vertex on the fringe and an empty tree, perform the following operation until fringe is empty.

Move an edge from the fringe to tree. If the vertex to which it leads is unvisited, visit that vertex, and put onto the fringe all edges that lead from that vertex to unvisited vertices.

This general method may not be as efficient as we would like because the fringe might become cluttered up with edges that points to vertices that are moved to the tree during the time that the edge is on the fringe.

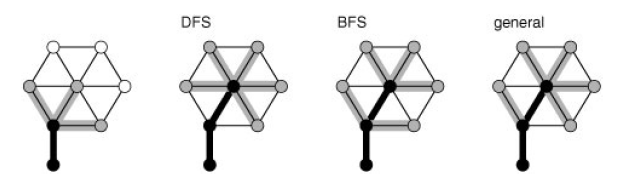
FIFO queue avoid it by making destination vertices when we put edge is on queue. We ignore edges to fringe vertices because we know that they will never be used. The old ones get off the queue before the new one does.

For stack implementation, we want opposite : when a edge is to be added to fringe that has the same destination vertex as one already there, we know that the old edge will never be used, because the new one will come off the stack before the old one.

To encompass these two extremes and to allow for fringe implementation that can use some other policy to disallow edges on fringe that points to the same vertex, we modify our general scheme as follows.

Move an edge from the fringe to the tree. Visit the vertex that it leads to, and put all edges that lead from that vertex to unvisited vertices onto the fringe, using a replacement policy on the fringe that ensures that no two edges on the fringe points to the same vertex.

image-20210113183833251

image-20210113183846616

Property 18.12 Generalized graph searching visits all the vertices and edges in a graph in time proportional to $V^2$ for the adjacency-matrix representation and to $V+E$ for the adjacency-list representation plus, in the worst case, the time required for $V$ insert, $V$ remove and $E$ update operation in a generalized queue of size $V$.

Program 18.10 Generalized Graph Search

#include "GQ.cc"
template <class Graph>
class PFS : public SEARCH<Graph>
{
    vector<int> st;
    void searchC(Edge e)
    {
        GQ<Edge> Q(G.V());
        Q.put(e); ord[e.v] = cnt++;
        while(!Q.empty()){
            e = Q.get(); st[e.w] = e.v;
            typename Graph :: adjIterator A(G, e.w);
            for(int t = A.beg(); t != A.end(); t = A.nxt())
                if(ord[t] == -1)
                { Q.put(Edge(e.w, t)); ord[t] = cnt++;}
            	else
                    if(st[t] == -1) Q.update(Edge(e.w,t));
        }
    }
    public:
    PFS(Graph &G) : SEARCH<Graph> (G), st(G.V(), -1)
    { search(); }
    int ST(int v) const { return st[v]; }
};

Program 18.11 Random Queue Implementation

template <class Item>
class GQ
{
    private:
    vector<Item> s; int N;
    public:
    	GQ(int maxN) : s(maxN+1), N(0){ }
    	int empty() const
        { return N==0; }
    	void put(Item item)
        { s[N++] = item; }
    	void update(Item x){ }
    	Item get()
        {
            int i = int(N*rand()/ (1.0+RAND_MAX));
            Item t = s[i];
            s[i] = s[N-1];
            s[N-1] = t;
            return s[--N];
        }
};

2 useful alternatives to BFS and DFS is

  1. using randomized queues in which we remove items randomly. Using it we get a search algorithms where each vertex on fringe is equally likely to be added to tree.
  2. Use a priority-queue ADT for fringe. We assign priority to each edge on fringe and update appropriately according to priority and add then them to tree.

All generalized graph-searching algorithm examine each edge just once and take extra space proportional to V in worst case; they do differ, however, in some performance measures.

image-20210113185747705