Special Graph
Some basic graph problems have simpler/faster polynomial algorithms if the given graph is special.
Directed Acyclic Graph
DAG is special graph with property : Di-rected and has no cycle. DAG implies no cycles by definition. That makes it suitable for solving problems using Dynamic Programming. Cyclic States or Dependency hurts DP at its core. We can view DP states as vertices in an implicit DAG and acyclic transition between DP states as directed edges of that implicit DAG. Topological sort allows each overlapping subproblem to be prcessed just once.
SSSP/SSLP on DAG
This problem becomes very simple since DAG has atleast one topological order ! we can use an O(V+E) topological sort algorithm to find one such order, then relax all the outgoing edges of these vertices according to this order. And we can find shortest path in just O(V+E) linear pass! This is also the essence of DP :).
Solving SSLP from starting vertex s to other vertices. The decision of this problem is NP-complete on general graph. However problem is easy if graph has no cycle. Just multiply all weights by -1 and negate the final result to get the answer.
Counting Paths in DAG
The number of paths can be found easily by computing one(any) topological order in O(V+E) (in this problem, vertex 0/birth will always be the first in topological order and vertex n/death will always be last). We start by setting num_paths[0] = 1. Then we process remaining vertices one by one according to the topological order. When processing a vertex u, we update each neighbor v of u by setting num_paths[v] += num_paths[u]. After such O(V+E) steps, we will know the number of paths in num_paths[n].
Bottom-Up versus Top-Down Implementation
For all three solutions for shortest/longest/counting paths on DAG above are Bottom-Up DP solutions. We start from base case (source) and then we use topological order of DAG to propogate the correct information to neighboring vertices without the need of backtrack.
It can also be written in Top-Down fashion. Let numPaths(i) : be the number of paths starting from vertex i to destination n.
- numPaths(n) = 1 // at destination n, there is only one path
- numPaths(i) = $\Sigma_j numPaths(j),\ \forall j$ adjacent to i.
To avoid recomputation we memoize the number of paths for each vertex i. There are O(V) distinct states and each vertex is processed only once so Complexity is same.
Converting General Graph to DAG
Sometimes its not directly DAG unless we do some modification :
SPOJ 0101 : Fishmonger
Abridged problem statement : Given number of cities 2 < n < 51, available 0<t<1001, and two nxn matrices (once gives travel times and another gives tolls between two cities), choose a route from port city (vertex-0) in such a way that the fishmonger has to pay as little as toll as possible to arrive at the market city(vertex n-1) within certain time t.
There are two potentialy conflicting requirements here. The first in to minimze tolls along the route and second is ensuring person reaches on time. Second requirement is hard constraint for this problem. that is, we must satisfy it, otherwise we don’t have a solution.
However is we attach a parameter t_left to each vertex then the given graph turn into DAG as in figure 4.35.
We start at vertex(port,t) in the DAG. Every time fishmonger moves from a current city cur to another city X, we move to a modified vertex (X, t- travelTime[curr][X]] in the DAG via edge with weight toll[cu][x] As this time is a diminishing resource we will never encounter a cyclic situation
ii go(int cur, int t_left) {
if(t_left < 0) return ii(INF,INF);
if(cur == n-1) return ii(0,0);
if(memo[cur][t_left] != ii(-1,-1))
return memo[cur][t_left];
ii ans = ii(INF, INF);
for(int X = 0; X < n; X++) if(cur != X) {
ii nextCity = go(X, t_left-travelTime[cur][X]);
if(nextCity.first + toll[cur][X] < ans.first) {
ans.first = nextCity.first + toll[cur][X];
ans.second = nexCity.second + travelTime[cur][X];
}
}
return memo[cur][t_left] = ans;
}
Minimum Vertex Cover (on a Tree)
The tree data structure is also an acyclic data structure. But unlike DAG there are no overlapping subreees in a tree. Thus there is no point in using DP.
But sometimes we maybe able to convert it into DAG. Such problems are called as ‘DP on tree’ problems in competitive programming.
An example of this DP on Tree problem is the problem of finding minimum vertex cover (MVC) on a tree. In this problem, we select the smallest pssible set of vertices C$\in$V such that each edge of the tree is incident to atleast one vertex of the set C. For the sample tree, the solution is to take the vertex 1 only because all edges 1-2, 1-3, 1-4 are all incident to vertex 1.
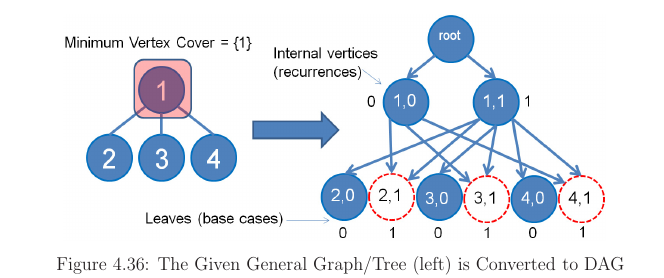
Now there is only two possibilities for each vertex. Either its taken or its not. By attaching this status to a vertex we can convert tree into DAG. If current vertex is not taken, then we take the best between taking or not taking its children. We can now write this top down DP recurrence : MVC(v,flag)
answer is min(MVC(root,false), MVC(root,true)). But we quickly have twice states now :).
int MVC(int v, int flag) {
int ans = 0;
if(memo[v][flag] != -1) return memo[v][flag];
else if (leaf[v])
ans = flag;
else if (flag == 0){
ans = 0;
for(int j = 0; j < (int) Children[v].size(); j++)
ans += MVC(Children[v][j],1);
}
else if(flag == 1) {
ans = 1;
for(int j = 0; j < (int) Children[v].size(); j++)
ans += min(MVC(Children[v][j],1), MVC(Children[v][j],0));
}
return memo[v][flag] = ans;
}
Tree
Tree is a special graph with the following characterstics : It has E = V-1, with no cycle, it is connected, and there exists one unique path for any pair of vertices.
Tree Traversal
DFS and BFS algorithms for traversing a general graph. If the given graph is rooted binary tree there are simpler traversal algorithms like pre-order, in-order and post-order traversal. (level-order ~ BFS).

Finding Articulation Points and Bridges in Tree
we have seen O(V+E) Tarjan’s DFS algorithm for finding articulation points and bridges of a graph. However if the graph is tree, the problem becomes simpler.
All edges on a tree are bridges and all internal vertices (degree > 1) are articulation poitns. O(V) as we have to count the number of internal vertices but code is much simpler.
SSSP on weighted Tree.
we have seen two algorithms for this O((V+E) log V) Dijkstra and O(VE) Bellman Ford for solving SSSP on graph. But on tree it becomes simpler. Any O(V) graph traversal algorithm i.e. BFS/DFS can solve this problem as path is always unique :) and its the shortest path.
APSP on weighted Tree
we have used O(V^3) Floyd Warshall’s for this in graphs. However in weighted tree, the APSP probelm is just repeat SSSP on weighted tree V times setting each vertex as source vertex one by one leading to complexity of O(V^2).
Diameter of Weighted Tree
We would have done O(V^3) floyd warshall for APSP and another O(V^2) to find the farthest pair.
However if the graph is tree problem becomes simpler. We only need 2 O(V) traversal : Do DFS/BFS from any vertex s to find the furthest vertex x, then do BFS/DFS one more time from x to get the true furthest vertex y from x. The unique path between x and y is diameter of tree.
Eulerian Graph
An Euler path is defined as a path in a graph which visits each edge of graph exaclty once. Similarly tour/cycle is an Euler Path which starts and ends on the same vertex. A graph which has either a Euler Path or Euler tour is called as Euler Graph.
Eulerian Graph Check
for Euler Tour, Just check if all vertices have even degree. It is similar for Euler path, i.e. an undirected graph has an Euler path if all except two vertices have even degrees. This euler path will start from one of these odd degree vertices and end in another. Such check can be done in O(V+E).
Printing Euler Tour
It requires little more work :) but code is given below.
list<int> cyc;
// list for fast insertion in the middle
void EulerTour(list<int>::iterator i, int u) {
for(auto v:adj[u])
if(v.second) {// if this edge can be used/not removed
v.second = 0; // indicates removed edge
for(auto uu : adj[v.first]){
if(uu.first == u && uu.second) {
uu.second = 0; // remove bi-directional edge
break;
} }
EulerTour(cyc.insert(i,u),v.first);
} } }
// inside int main()
cyc.clear();
EulerTour(cyc.begin(), A);
for(list<int>::iterator it cyc.begin(); it!= cyc.end(); i++)
printf("%d\n",*it);
Bipartite Graph
Bipartite Graph is a special graph with following characters : the set of vertices V can be partitioned into two disjoint set V1 and V2 and all edges in (u,v) $\in$ E has the property that $u\in V_1$ and $v\in V_2$. This makes Bipartite Graph free from odd-length cycles. Note Tree is also Bipartite Graph.
MCBM (Max Cardinality Bipartite Matching) and Its Max Flow Solution
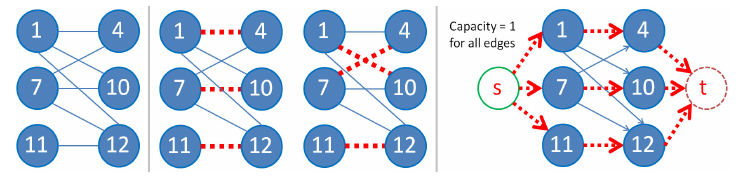
Given a list of numbers N, return a list of all the elements in N that that can be paired with N[0] sucessfully as a part of a complete prime pairing, sorted in ascending order. Complete prime pairing means that each element a in N is paired to a unique other element b in N such that a + b is prime.
N = {1,4,7,10,11,12} solution is {4,10}. We can take 4 and N[0] = 1 to make 5 (a prime) and then we can match pairs for rest of number s.t. sum of those pairs is prime namely (7,10) and (11,12). for 10 we have (1,10) , (4,7), (11,12) but for 12 we don’t have any other prime pair other than (1,12).
Constraint : List N contains even number of elements ([2…50]). Each element of N will be in range (1,1000) . Each element of N is distinct.
Althought this problem involves prime numbers its not a pure mathematical problem, as the elements of N are not more thank 1k- there are not too many primes belowe 1000 (only 168). The issue we cannot do complete pair searching as there are $\C_2^{50}$ possibilties for first pair and $\C_2^{48}$ for the second and so on.DP with bitmasking technique is also not usable as 2 ^50 is too big.
The key to solve this problem is that it is a pairing (matching) problem done on bipartite graph. To get a prime number we sum 1 odd + 1 even.
So we can split numbers into two sets set1/set2 s.t. one set is even and another is odd and we add an edge only if i->j set[i] + set[j] is prime.
If this graph is built : then if size of set 1 != set2 no such pairing is possible. Otherwise , if the size of both set are n/2 try to match set1[0] with set2[k] for k = 0..n/2-1 and do Max Cardinality Bipartite Matching.
If we obtain n/2-1 more matching add set2[k] to answer. For this test case answer is {4,10}.
MCBM problem can be reduced to max flow problem by assigning a dummy source vertex s connected to all vertices in set1 and all vertices in set2 connected to a dummy sink vertex t. By setting capacities of all edges in this flow graph to 1, we force each vertex is set1 to be matched with at most 1 vertex in set2. The max flow will be equal to the maximum number of matchings on the original graph
Max Independent Set and Min Vertex Cover on Bipartite Graph
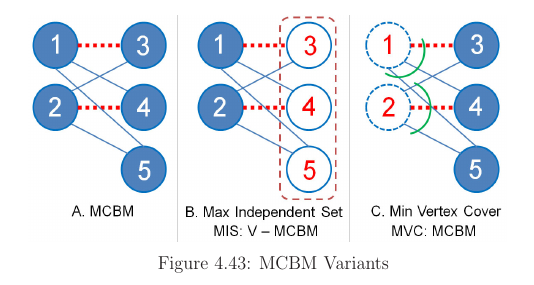
An independent set (IS) of a graph G is a subset of vertices s.t. no two vertices in the subset represent an edge of G. A Max IS (MIS) is an IS s.t. adding any other vertex to the set causes the set to contain an edge. In Bipartitie Graph, the size of MIS + MCBM = V. Or in another word: MIS = V - MCBM. In figure 4.43B, we have a Bipartite Graph with 2 vertices on the left side and 3 vertices on the right side.
The MCBM is 2 (dashed lines) and MIS is 5-2 = 3. Indeed {3, 4, 5} are members of the MIS of this Bipartite Graph. Another term is Dominating Set
A vertex cover of graph G is a set C of vertices such that each edge of G is incident to atleast one vertex in C. In Bipartite Graph, the number of an MCBM equals to the number of vertices in Min Vertex Cover (MVC) - this is theorem by a Hungarian mathematician Denes Konig.
A point to note that the MCBM/MIS/MVC values are unique, the solutions may not be unique.
Sample Application UVa 12083 - Guardian of Decency
Abridged Problem Description : Given N < 500 students (in terms of height, gender, music style and favorite sport), determine how many students are eligible for an excursion if the teached wants any pair of two students to satisfy at least one of these four criteria so that no pair of student becomes a couple.
1 ) Their height differs no more than 40 cm. 2) They are of same sex. 3) Their preferred music style is different. 4) Their favorite sport is the same.
First notice problem is all about finding MIS i.e. the chosen students should not have any chance of becoming a couple. Independent set is a hard problem in general in graph, so let’s check if he graph is special. Next notice that there is an easy Bipartite Graph in the problem description : The gender of students (constraint number 2). We can put the male students on the left and female students on right. At this point we should consider what should be edges of this BipartiteGraph
The answer is related to Independent Set Problem : we draw an edge between a male student i and a female student j if there is a chance that (i,j) may become couple.
In this contect of this problem. If i and j have DIFFERENT gender and their height differs by NOT MORE than 40 cm and their preffered music style is THE SAME and their favourite sport is DIFFERENT, then this pair, one male student i and one-female student j, has a high probability of becoming a couple. The teacher can choose one of them. Now, once we have this Bipartite Graph, we can run MCBM algorithm and report : N - MCBM.
Augmenting Path Algorithm for Max Cardinality Bipartite Matching
There is a better way to solve the MCBM problem in contest (in term of implementation) rather than going via ‘Max-Flow Route’. we can use the specialized and easy to implement O(VE) augmenting path algorithm. With this implementaion handy, all the MCBM problems, including other graph problems that require MCBM- like MIS in Bipartite Graph.
An augmenting path is a path that starts from a free (unmatched) vetex on the left set, alternate between a free edge (now on right side set), a matched edge (now of left set again)… , a free edge (now on right set) until the path finally arrives on a free vertex on the right set of Bipartite Graph.
Lemma : (Claude Berge 1957) A Matching in graph G is maximum (has the max possible number of edges) if and only if there is no more augmenting path in G. This augmenting path algorithm is a direct implementation of Berge’s Lemma. Find and then eleminate augmenting paths.
Algorithm repeats O(E) DFS-like code V times, it runs in O(VE). Its not best algorithm for MCBM. we can study Hopcropt Karp’s algorithm that solve MCBM in $O(\sqrt V E)$.
vi match, vis; // globals
int Aug(int l) { // return 1 if there is augmenting path
if(vis[l]) return 0; // return 0 otherwise
vis[l] = 1;
for(auto r : adj[l]) {
if(match[r] == -1 || Aug(match[r])) { // edge weight not needed
match[r] = l; return 1;
} }
return 0; // no matching
}
// inside int main ()
int MCBM = 0;
match.assign(V,-1); // V is number of vertices
for(int l = 0; l < n; l++) { // n - size of left set
vis.assign(n,0); // reset before each recursion
MCBM += Aug(l);
}
printf("Found %d matchings\n", MCBM);