DP 1

This is long sections divided into 3 parts. Its very important for interviews.

In recursion we say subproblems were related to the original problems does they always have to be ? Should they be in recurrence relation to each other.

Sometimes we do not need to do that necessarily.

What Dynamic Programming is => DnC ( divide and conquer) + something extra …

what this extra is ?

Climbing Stairs :

User stands at bottom , he has a choice of making 1 step or 2 steps , how many ways he can reach top (n stairs).

Again lets say he jumps 1 step but the problem again we can ask same question but size of stairs is n-1 now. Or he takes 2 steps then we ask how many steps to do same for n-2 stairs.

f(n) = f(n-1) + f(n-2)

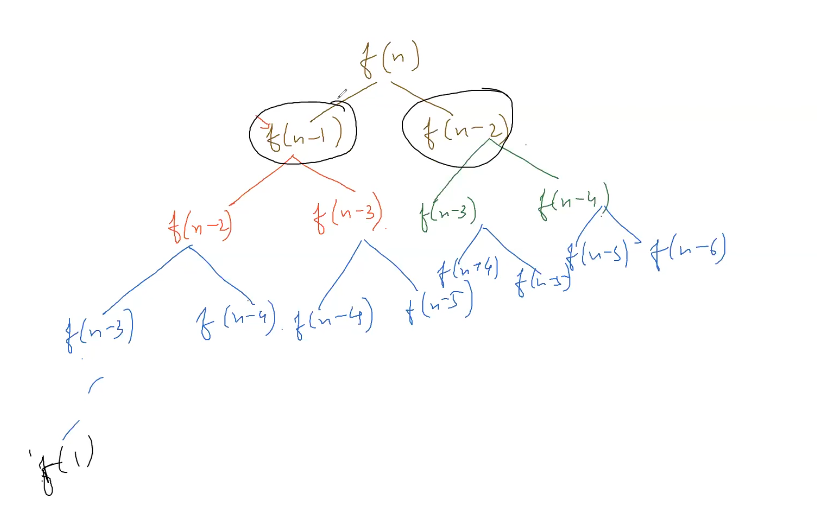
image-20210421091111426

So we see that we are computing a lot of calls to function again and again. We can improve the runtime by saving the result of previous calls in some way to quickly look it up otherwise go into recursion. This is known memoization.

This is the extra step… :) storing solution to these subproblems.

lets create a framework for pursuing problems easily

  • Divide and Conquer ( come up with recurrence )

    1. come up with a criteria ( decision ) to split the result into mutually disjoint $(s1 \and s2 = \phi )$ and exhaustive set $(s1 \or s2 = U )$

      • Types of problem
        • Enumeration ( backtracking )
        • Counting Problem ( this problem xD )

    2. Here $x_1 $ : # ways to reach top thru the 1 st floor

      Here $x_2 $ : # ways to reach top thru the 2 nd floor

    3. Combine both to get original problem

      Recurrence : f(n) = f(n-1) + f(n-2);

    4. Base Cases : f(1) = 1, f(2) = 2

  • Extra Part : Memoization

    Draw the recursion tree ( 2 levels ) and see if the subproblems are recurring

    If it is the case then its DP problem

    1. Store the solution to subproblems
    2. Looking them up whenever you are solving a subproblem.

lets see how we design the storage in step 1. we say only one variable n that defines subproblems and then check size of n then we can in this case easily we can say use a array.

default value on data structure for step 2. so lookup always is all about checking the data structure if its initialized means we have to solve otherwise we take data from here.

So default value never should be a possibility of answer. Here ‘0’ sounds like a good initial value.

int climbStairsHelper(int n, vector<int>& dp){
    // base case
    if(n == 1) return 1;
    if(n == 2) return 2;

    // recursive step
    // check the table
    if(dp[n] != -1)
        return dp[n];

    // if not solved
    // solve now and store in table
    dp[n] = climbStairsHelper(n-1,dp) + climbStairsHelper(n-2,dp);
    return dp[n];
}
int climbStairs(int n) {
    vector<int> dp(n+1,-1);
    return climbStairsHelper(n,dp); }

Now lets do some Time Complexity Analysis

Recurrence : $O(2^n)$

Memoization : $O(n)$ with a cost of $O(n)$ space.

Here if we observe we are looking the table quite a lot of times, we can make it from smallest to largest then we don’t even have to check the dp[n] we are guaranteed to get the solution of subproblem.

int climbStairs(int n) {
    if(n == 1) return 1;
    vector<int> dp(n+1,-1);
    dp[1] = 1;
    dp[2] = 2;
    for(int i = 3; i < n+1; i++)
        dp[i] = dp[i-1]+dp[i-2];
    return dp[n];
}

do we need the table entire time xD :) just take 2 variables or a table of 2 variables and use mod to cycle the values. :)

1D Subproblems

House Robber :

Robber can’t rob adjacent houses. Determine houses he will rob to get maximum money.

How to identify this is a DP problem

  • Optimization
  • Counting ( different from enumeration )

Lets first do DnC(divide n conquer) and come up with recurrence and then use the memoization.

  1. Criteria

For enumeration finding criteria was easy : first solution contained x and second doesn’t contain x , here we are given optimization problem and answer is one final answer.

So we can say optimal solution contains x or it doesn’t contain x

Say here optimal solution is [$H_i,\ H_j, \ H_k … $] we can $H_1 $ is either the part of the solution or it is not dividing all possible configuration in 2. so check there are mutually exclusive and mutually exhaustive.

Question askes for the configuration that gives maximum sum which is nothing but max{S} = max{max{s1},max{s2}}

where s1 , s2 are possible configurations. s1 includes $H_1 $ and s2 doesn’t

  1. Relate these subproblems to original problem

P( A , 0, n-1) : problem for all houses…

p1 : M(H_1) + P (A,2,n-1) (// include the constraint of nearest house can’t be included)

p2 : P(A,1,n-1)

  1. Mathematically represent the subproblems

P : f(A,0,n-1)

P1 : M(H_1) + f(A,2,n-1)

P2 : f(A,1,n-1)

  1. Nature of Subproblems - > how these subproblems related to original problem

These all are suffix array of problem.

decide the dimension of problem (number of variable needed to solve the subproblem ) -> use starting index to define suffix array

  1. Recurrence

    P(A,0) = max{A(0) + P(A,2) , P(A,1)}

  2. Base Cases ( Smallest Subproblem)

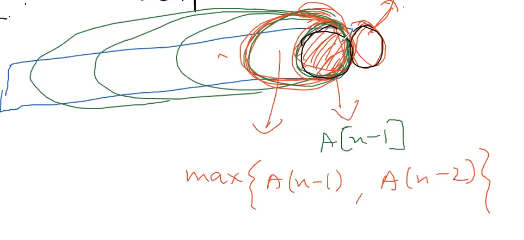
    image-20210421114458579

    while solving for last 2 elements its nothing but max{A(n-1), A(n-2)} or we can last element A(n-2)

Extra Solution : Check we need memoization , draw the tree

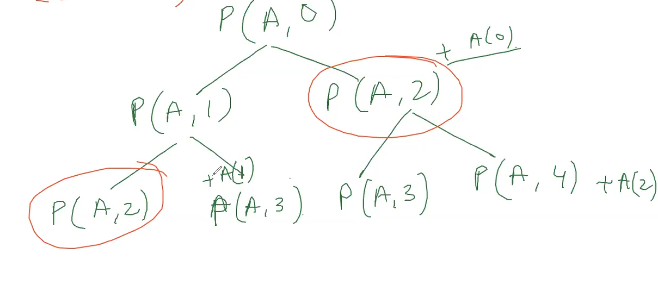
image-20210421114709643

Voila ! they are repeating indeed.. :) Overlapping Subproblems!

  1. Design of Data Structure for answering the subproblem

    • Size : # subproblems -> (nature suffix array) -> n ( 1 dimensional )

      dp[i] : P(A,i)

    • order of filling

      • either fill in order of recurrence tree, decide a default value : -1
      • from smallest subproblem to largest subproblem
//<data-type of ans> f(<Subproblem representation>,<DP table>)
int robHelper(vector<int>& nums,int start,vector<int>& dp){
    int n = nums.size();
    // base cases
    if(start == n-1)
        return nums[n-1];
    if(start == n)
        return 0;
    // check the dp table
    if(dp[start] != -1)
        return dp[start];
    // recursive call
    dp[start] = max(nums[start]+robHelper(nums,start+2,dp),
                    robHelper(nums,start+1,dp));
    return dp[start];  }
int rob(vector<int>& nums) {
    int n = nums.size();
    vector<int> dp(n+1,-1);
    return robHelper(nums,0,dp); }

Second Approach :

Smallest subproblem to largest subproblem

int rob(vector<int>& nums) {
    int n = nums.size();
    vector<int> dp(n+1,-1);
    dp[n] = 0, dp[n-1] = nums[n-1];
    for(int i = n-2; i >= 0; i--)
        dp[i] = max(nums[i]+dp[i+2], dp[i+1]);
    return dp[0]; }

We prefer Second Approach since it sometimes offers State space Optimization :

See here we can see that we need i,i+1, i+2 only to solve the problem and just maintain 3 variables.

Another way to do the solution

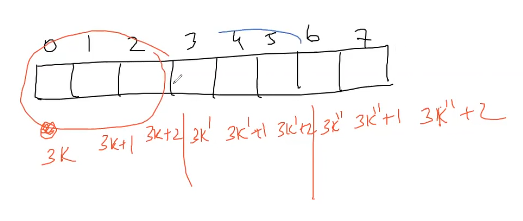
image-20210421120551846

instead of 3 variables and using this fact that we can group them in groups of 3 and take modulo on vector of 3 elements. or 2 will also do fine if we are careful enough and actually taking 2 of them makes sense since we need only i +1 and i+2 that i index used is from nums :)

int rob(vector<int>& nums) {
    int n = nums.size();
    vector<int> dp(2,-1);
    
    dp[n%2] = 0, dp[(n-1)%2] = nums[n-1];
    for(int i = n-2; i >= 0; i--)
        dp[i%2] = max(nums[i]+dp[(i+2)%2], dp[(i+1)%2]);
    return dp[0%2];
}

Solution of Climbing Stairs using this approach : http://p.ip.fi/a6qS

Lets try the robber 2

House Robber II : Try similar problem with constraint changed.

Best Time to Buy and Sell Stocks with Transaction Fee : might look like above problems but its not because we can sell at will.