Graphs 4
Disjoint Data Structures
Lets traverse input and construct graph.
$ I = [e_1, e_2,…,e_n]$ : These are edges and now we consider we have some $m$ nodes
Now traverse $I$ and add edges to nodes and we keep checking the cycles at each addition. Every edge that is added and causes cycle is the redundant!
So Basically problem is keeping a set of nodes and connecting them and checking the cyclicity at each addition.
Forest : set of Trees.
We need a way to represent these independent connected nodes (trees).
In tree each node has only one parent. Then we can maintain a parent array.
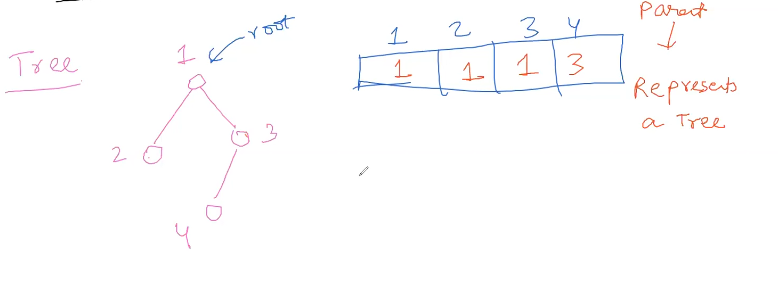
Now how can we represent set of trees ?
For example :
let say $ I = [[1,2], [2,3] , [3,4], [1,4], [1,5]]$
then our array : $A = [1,2,3,4,5]$
Here idx(1) = 1 means node is parent of itself.
$ A = [1,1,3,4,5]$ after adding 2
$A = [1,1,1,4,5]$ after adding 3 (note we add only parents of nodes while adding)
$A = [1,1,1,1,5]$
$A=[1,1,1,1,1]$
so basically all nodes are interconnected! or all have common parent
Now question is how to detect cycle Now say if there are 2 nodes we are going to connect have same root that means that they are part of same tree and connecting them gives cycles (pretty straightforward).
getting to root using the parents array is recursive step!
int findRoot(vector<int>& parent, int x){
int curr_node = x;
while(parent[curr_node] != curr_node)
curr_node = parent[curr_node];
return curr_node;
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
vector<int> parent(n+1,-1);
// Start with an empty set of trees
for(int i = 1; i <= n; i++)
parent[i] = i;
// Add edges one by one
for(int i = 0; i < n; i++){
int x = edges[i][0];
int y = edges[i][1];
int root_x = findRoot(parent,x);
int root_y = findRoot(parent,y);
if(root_x == root_y)
return edges[i];
parent[root_y] = root_x;
}
// NF.
return {-1,-1};
}
Note : there is only redundant edge as $N$ edges and $N$ nodes so there is 1 edges causing cycle.
This kind of data structure is known as Disjoint Data Structure!
So in this case sets were tree!
At any point we needed 2 operation! We were connecting root : Union
and we were finding the root of a node : Find
So this data structure is also known as $union-find$ Data Structure.
Potential Application!
- Cycle Detection
- Connectivity
Number of Operations to Make Network Connected
Find the number of connected components and number of extra edges connected (edges from cycle) answer is expression in form of these numbers.
Any more than $n-1$ edges in $n$ edge graph causes cycles we use this fact and tell number of connected components.
class DisjointSet{
public:
// constructor.
DisjointSet(int len){
parent.resize(len);
for(int i = 0; i < len; i++)
parent[i] = i;
num_components = len;
}
void union_(int x, int y){
int r_x = find_(x);
int r_y = find_(y);
parent[r_x] = r_y;
num_components--;
}
int find_(int x){
while(x != parent[x])
x = parent[x];
return x;
}
int getNumComponents(){
return num_components;
}
private:
vector<int> parent;
int num_components;
};
class Solution {
public:
int makeConnected(int n, vector<vector<int>>& connections) {
DisjointSet ds(n);
int extra_edge_count = 0;
// Keep adding edges.
for(int i = 0; i < connections.size(); i++){
int x = connections[i][0];
int y = connections[i][1];
// Extra edge ?
if(ds.find_(x) == ds.find_(y))
extra_edge_count++;
else
// connect.
ds.union_(x,y);
}
int num_components = ds.getNumComponents();
if(num_components-1 > extra_edge_count)
return -1;
return num_components-1;
}
};
Can we do better than this!
Or say union criteria can be use height of tree for comparison to remove linear chains of tree! This is called as Union by Rank
Other thing that is important is called as Path Compression. When we are finding parents we can compress the path also.
Directly connect nodes to root so root becomes the parent of all, but wait how u now that particular node is root! :)
While recurring change the links!!
Spanning Tree
For a graph, ST of a graph is a tree that spans all the vertices of the graph.
(Removing any edge makes it spanning tree or smallest subgraph that is connected)
Minimum Spanning Tree : Sum of weights of edges ! is minimum.
How we compute MST(weighted)
Can we use Disjoint set ?
-
sort all edges by weights
-
traverse from smallest edge weight to largest
- Add edge to DS if it doesn’t form a cycle
Above is a greedy strategy!
And this is called as Kruskal’s Algorithm
Another way! ? Shortest-Path ?
Any SPSP Algorithm (Dijkstra) gives you MST.
or using searching for smallest weight on BFS (Prim’s Algorithm)
Optimize water Distribution in a Village
There are $n$ houses in a village. We want to supply water for all houses by building wells and pipes.
For each house $i$ , we can either build a well inside it directly with cost walls[i-1] {-1 : due to zero indexing } , or pipe in water from another well to it. The cost of laying pipe is given by array pipes where
pipes[j] = [$house1_j , house2_j , cost_j$] representing cost of connecting house1 to house2, together using pipe. Consider connection are bidirectional.
Return the minimum total cost to supply water to all houses.
Since problems indicates all houses should have water supply that means this problem is related to minimum spanning tree.
Review and Time-Space Complexity Analysis
-
Motivation the need for graph
$I_1, R, I_2$ -> Graph
Represent : $I_1$ : vertices
R : Edges
-
Implementation of Graph
- Adjacency Matrix
A[i][j]=1representing $v_i Rv_j$- Problem of data sparsity : less edges
- Adjacency List
- Problems of dense graphs
- Adjacency Matrix
-
R : Relation
- Directed v/s Undirected
- Weighted v/s Unweighted
-
Graph Exploration ( Traversal )
-
DFS : depth first search
-
BFS : level order
-
Maintaining a visited list / array to store vertices already visited.
-
Time Complexity
-
DFS : $O(|E|)$ generally but if #edges < #vertices ( connected components) then $O(|V|)$ so generally $O(|E|+|V|)$
Note $O(max(a,b)) = O(a+b)$
-
-
-
Graph Algorithm
-
Connectivity
- Graph is connected / not : $O(|E|+|V|)$
- #connectivity components : $O(|E|+|V|)$
-
Cyclicity
- Undirected : $O(|E|+|V|) $: maintained only visited array
- Directed : $O(|E|+|V|)$: along with visited array we needed to track current path.
- DAG : Topological Sorting : maintained indegree and decreased on visiting neighbors : based on BFS
-
Shortest Path
-
SPSP : Single Pair shortest Path
- Unweighted : BFS
- Weighted : Dijkstra
- Weighted BFS : used priority queue with carrying the weight.
- pop from PQ
- Traverse all never and pushing for every unvisited edge
- Complexity $O(|E| \log N)$ N : is size of PQ
- There were 2 approaches to
- Push the vertex irrespective
- When pop if already visited ignore
- Upper bound on size of PQ is $|E|$
- In worst case it will become $O(|V|+|E|) \log |E|$
- Upper bound on $|E| = O(|V|^2)$
- Overall $O(|E| \log |V|)$
-
APSP : All pair shortest path
-
unweighted : Floyd Warshall
-
$O(|V|^3)$ DP Solution! : good for dense graph as edges are more : Floyd Warshall
-
using SPSP on all $|V|$ vertices : $O(|E||V|\log |V|)$ : good for sparse graph Dijkstra
-
-
weighted : same as above
-
-
-
Tarzan’s Algorithm for bridges : use rank vector
- Fundamentally BFS : $O(|E| \log |V|)$
-
Disjoint Set
- union and find
- worst case : linear tree but we can use height tree to limit height
- or we could use path compression.
-
Spanning Trees
-
MST :
-
Kruskal : Average $O(\log N)$ using optimization without it average
$O(|E| \log |E|)$
-
Prim’s Algorithm : Variation of Dijkstra so its $O(|E|\log |V|^2)$
-
-
-