5-Properties of trees
Mathematical properties of Binary Trees
Property:1 A binary tree with N internal nodes has N+1 external nodes
Property:2 A binary tree with N internal nodes has 2N links: N-1 links to internal nodes and N+1 links to external nodes
Note : performance characterstics of a lot of algorithms depends not only on number of nodes in associated trees, but on various structural properties.
Definition The level of a node in a tree is one higher that the level of its parent(with the root at level 0). The height of tree is the maximum of the levels of all the tree’s nodes.
The internal path length of a binary tree is the sum of the levels of all the tree’s internal nodes.
The external path length of a binary tree is the sum of the levels of all the tree’s external nodes.
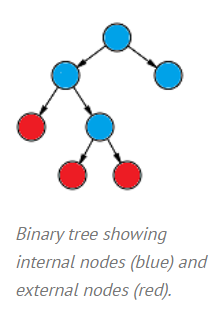
Property:3 External path length of any binary tree with N internal nodes is 2N greater than the internal path length.
Property:4 The height of a binary tree with N internal nodes is at least lg N and at most N-1.
Example for 10 internal nodes tree.
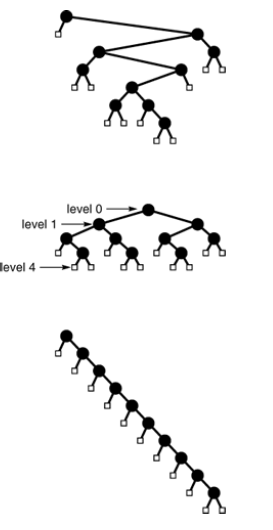
$ 2^h-1 < N + 1 \le 2^h $
Property: 5 The internal path length of a binary tree with N internal nodes is at least Nlg(N/4) and at most N(N-1)/2