7-Simple Euler and Hamilton Paths
Simple, Euler, and Hamilton Paths
Program 17.16 Simple Path Search
template <class Graph> class sPATH
{
const Graph &G;
vector<bool> visited;
bool found;
bool searchR(int v,int w)
{
if(v==w) return true;
visited[v] = true;
typename Graph::adjIterator A(G,v);
for(int t = A.beg(); !A.end(); A.nxt())
if(!visited[t])
if(searchR(t,w)) return true;
return false;
}
public:
sPATH(const Graph &G, int v, int w) :
G(G), visited(G.V(), false)
{found = searchR(v,w); }
bool exists() const
{ return found; }
};
Problem of finding the path in a graph takes us away from local properties such as existence of edges/ degree of vertices to global properties that tell us about a graph’s structure.
The most basic such property is whether two vertices are connected. If they are then finding path in between them.
Trace for finding path from 2 to 6
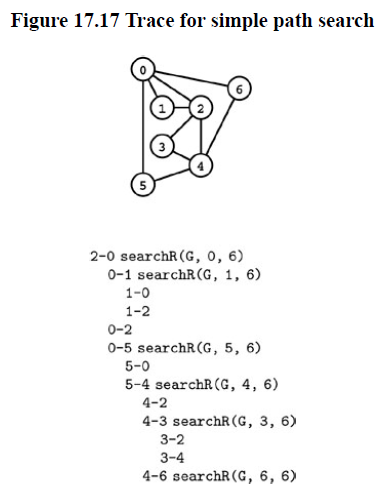
Simple Path : Given two vertices, is there a simple path in the graph that connects them ?
Program 17.16 is direct solution that finds path and based on dfs. How we can make it print the path.
- Add a statement to print t-v just after the recursive call in searchR finds a path from $t$ to $w$
- Switch w and v in the call on searchR in the constructor.
First change prints the path in reverse order and second reverses that order.
Property 17.2 : We can find a path connecting two given vertices in a graph in linear time.
In worst case it checks all entries in the adjacency matrix exactly once.
Hamilton Path : Given two vertices, is there a simple path connecting them that visits every vertex in the graph exactly once ? If the path is from a vertex back to itself, this problem is known as the Hamilton Tour.
Program 17.17 Hamilton Path
bool searchR(int v, int w, int d)
{
if(v==w) return (d==0);
visited[v] = true;
typename Graph::adjIterator A(G,v);
for(int t = A.beg(); !A.end(); t = A.nxt())
if(!visited[t])
if(searchR(t,w, d-1)) return true;
visited[v] = false;
return false;
}
Property 17.3 A recursive search for a Hamilton tour could take exponential time.
Proof : consider a graph where vertex V-1 is isolated and the edges, with the other V-1 vertices, constitutes a complete graph. Above program will never find a Hamilton path, but it is easy to see it will examine $(V-1)!$ paths in complete graph, all of which involve $V-1$ recursive calls. Total calls $V!$. or $(V/e)^V$, which is higher than any constant to the Vth power.
For checking there is a Hamilton Path we can directly check whether there is a Simple Path.
Factorial-time algorithms are too slow
If we could process a graph with 15 vertices in 1 second, it would take 1 day to process a graph with 19 vertices , over 1 year for 21 vertices, and over 6 years for 23 vertices. Faster computer don’t help much, either.
Euler Path : Is there a path connecting two given vertices that uses each edge in the graph exactly once ? The path need not be simple - vertices may be visited multiple times. If the path is from a vertex back to itself, we have a Euler tour problem. Is there a cyclic path that uses each edge in the graph exactly once ?
Property 17.4 : A graph has an Euler tour if and only if it is connected and all its vertices are of even degree.
Proof : First to reach all edges we need it to be connected and even because if we enter a node we want to leave on different edge.
Corollary : A graph has an Euler path if an only if it is connected and exactly two of its vertices are of odd degree.
Property 17.5 We can find an Euler tour in a graph, if one exists, in linear time.
Program 17.18 Euler path existence
template < class Graph> class ePATH
{
Graph G;
int v,w;
bool found;
STACK<int> S;
int tour(int v);
public:
ePATH(const Graph &G, int v,int w):
G(G), v(v), w(w) {
DEGREE<Graph> deg(G);
int t = deg[v]+deg[w];
if((t%2) != 0 ) { found = false; return;}
for(t = 0; t <G.V(); t++)
if((t!=v) && (t!=w))
if((deg[t] %2)!=0)
{found = false; return;}
found = true;
}
bool exists() const
{ return found;}
void show();
};
Program 17.19 Linear-time Euler Path (hard to understand )
template <class Graph>
int ePATH<Graph>::tour(int v)
{
while (true)
{ typename Graph::adjIterator A(G, v);
int w = A.beg(); if (A.end()) break;
S.push(v);
G.remove(Edge(v, w));
v=w;
}
return v;
}
template <class Graph>
void ePATH<Graph>::show()
{
if (!found) return;
while (tour(v) == v && !S.empty())
{ v = S.pop(); cout << “-” << v; }
cout << endl;
}