1-Glossary and Rules of Game
Digraphs and DAGs
when we attach significance to order in which the two vertices are specified in each edge of a graph, we have an entirely different combinatorial object know as a digraphs or directed graph.
One common situation is for the edge direction reflects a precedence relationship.
Another way to model the same situation is to use a PERT chart: edges represent jobs and vertices implicitly specify the precedence relationships How to decide when to perform each job, this is known as scheduling problem.
It makes no sense if the digraph has a cycle so, in such situations, we are working with directed acyclic graphs (DAGs). We will consider properties of DAGs and algorithms for scheduling and solving problem of topological sorting.
Number of possible digraphs is truly huge. for $V^2$ edges we have total $2^{V^2}$ possible graphs ( including self loops). There is much smaller number of classes of digraphs that are isomorphic to each other, but we can’t take advantage of this reduction because we do not know an efficient algorithm for digraph isomorphism.
Glossary and Rules of the Game
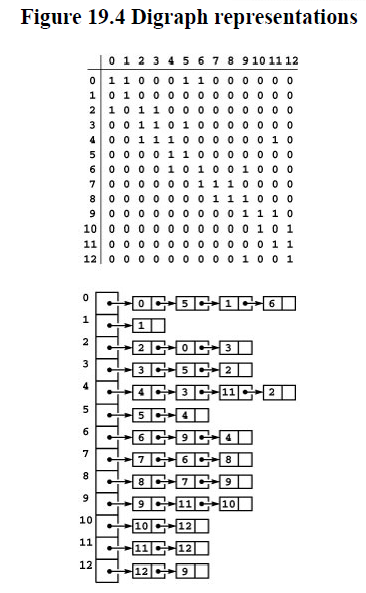
Definition 19.1 A digraph is a set of vertices plus a set of directed edges that connect ordered pairs of vertices (with no duplicate edges). We say that an edge goes from its vertex to its second vertex
Definition 19.2 A directed path in a digraph is a list of vertices in which there is a (directed) digraph edge connecting each vertex in the list to its successor in the list. We say that a vertex $t$ is reachable from a vertex $s$ if there is a directed path from $s$ to $t$
sink has outdegree 0. and source has indegree of 0.
A digraph where self-loops are allowed and every vertex has outdegree 1 is called a map(a function from the set of integers from 0 to $V-1$ onto itself.)
We can easily compute the indegree and outdegree each vertex, and find sources and sinks, in linear time and space proportional to $V$.
Program 19.1 Reversing a digraph
template <class inGraph, class outGraph>
void reverse(const inGraph &G, outGraph &R)
{
for(int v = 0; v<G.V(); v++)
{
typename inGraph::adjIterator A(G,v);
for(int w = A.beg(); w != A.end(); w = A.nxt())
R.insert(Edge(w,v));
}
}
Definition 19.3 A directed acyclic graph (DAG) is digraph with no directed cycles.
Definition 19.4 A digraph is strongly connected if every vertex is reachable from every vertex.
Only no DAG that contains more than one vertex is strongly connected.
This relation is transitive in nature if s is strongly connected to t, and t is strongly connected to u, then s is strongly connected to u.
Strong connectivity is a equivalence relation that divides the vertices into equivalence classes containing vertices that are strongly connected to each other.

Property 19.1 A digraph is not strongly connected comprises a set of strongly connected components (strong components, for short), which are maximal strongly connected subgraphs, and a set of directed edges that go from one component to another.
Property 19.2 Given a digraph D, define another digraph K(D) with one vertex corresponding to each strong component of D and one edge in K(D) corresponding to each edge in D that connects vertices in different strong components (connecting the vertices in K that correspond to the strong components that it connects in D) Then, K(D) is a DAG (which we call the kernel of D).
Connectivity We reserve the term connected for undirected graphs. In digraphs, we might say that two vertices are connected if they are connected in the undirected graph defined by ignoring edge directions, but we generally avoid these usages.
Reachability In digraphs, we say t is reachable from vertex s if there is a directed path from s to t. We generally avoid the term reachable when referring to undirected graphs, although we might consider it to be equivalent to connected because the idea of one vertex being reachable from another is intuitive in certain undirected graphs.
Strong Connectivity Two vertices are strongly connected if they are mutually reachable ; in undirected graphs, two connected vertices imply the existence of paths from each to the other. Strong connectivity in digraphs is similar in certain ways to edge connectivity in undirected graphs.