1-Digital Search trees

Radix Search Methods, operate in analogous to radix-sorting methods and are quite useful when pieces of search keys are accessible.

Depending on the context a key might a word (a fixed-length sequence of bytes) or a string (a variable-length sequence of bytes). We treat keys that are words as numbers in base R number system for various values of R (radix) and work with individual digits of the number.

We can view C-style strings as variable-length numbers terminated by a special symbol so that, for both-fixed and variable length keys we can base all out algorithms on the abstract operation “extract the $i^{th}$ digit from a key” including a convention to handle case that the key has fewer than $i$ digits.

Principal advantage is these methods provide reasonable worst-case performance without the complication of balanced trees.

Digital Search Trees (DSTs)

The search and insert algorithms are identical to binary trees except one difference : We branch in the tree not according to the result of comparison between the full keys, but rather according to selected bits of key. At first level, leading bit is used, at second level, the second bit is used; and so on, until an external node is encountered.

Rather than using < to compare keys, we assume that digit function is available to access individual bits in the keys.

Binary digital search tree

private:
	Item searchR(link h, Key v, int d)
    {
        if(h==0) return nullItem;
        if(v == h->item.key()) return h->item;
        if(digit(v,d)==0)
            return searchR(h->l,v,d+1);
        else searchR(h->r,v,d+1);
    }
public:
	Item search(Key v)
    { return searchR(head, v, 0);}

image-20210101095608329

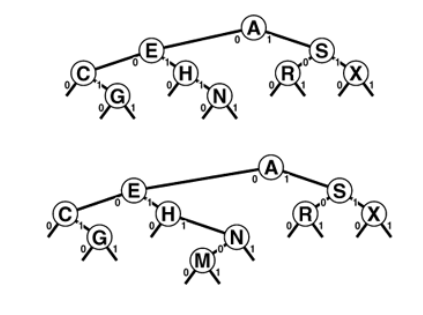
image-20210101095619841

The bits of the keys control search and insertion, but note that DSTs don’t have ordering property that characterises BSTs.

DSTs are characterised by property that each key is somewhere along the path specified by the bits of key(in order from left to right ).

if keys are words of fixed length, all consisting of w bits. Our requirement that keys are distinct implies that $N\le 2^w$, and we normally assume that N is significantly smaller than $2^w$ , since otherwise key-indexed search would be the appropriate algorithm to use.

The worst case for trees built with digital search is much better than that for binary search tree, if number of keys is large and length of keys are small relative to number of keys.

Property 15.1 A search or insertion in a digital search tree requires about $\lg N$ comparisons on the average, and about $2\lg N$ comparisons in the worst case, in a tree built from N random keys. The number of comparisons is never more than number of bits in the search key.