6-Tree Traversal

Tree Traversal

This function takes a link to a trees as an argument and calls function visit with each of the nodes in the tree as arguments.

Recursive tree traversal

void traverse(link h, void visit(link)){
    if(h==0) return;
    visit(h);
    traverse(h->l,visit);
    traverse(h->r,visit);
}

There can be three order in which we can traverse a node :

  • Preorder
    • where we visit node, then visit left and right subtrees
  • Inorder
    • where we visit the left subtree, then visit the node, then visit right subtree
  • Postorder
    • where we visit the left and right subtrees, then visit the node.

image-20200904184546387

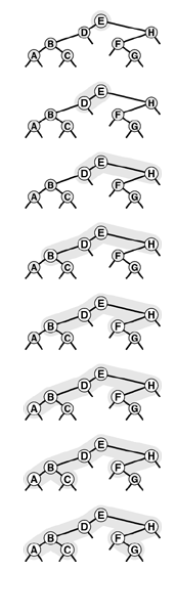
Three traversals depicted in order

Preorder Stack Call(leftmost)

image-20200904184627960

Doing inorder traversal is same as solving Towers of Hanoi.

Note doing the postorder traversal is equivalent to evaluating postfix expressions.

Non recursive implementation

void traverse(link h, void visit(link)){
    stack<link> s(max);
    s.push(h);
    while(!s.empty()){
        visit(h=s.pop());
        if(h->r !=0) s.push(h->r); // TO ensure we don't push empty links
        if(h->l !=0) s.push(h->l);
    }
}
  • For preoder , push the right subtree , then left and then node
  • For inorder, push the right subtree, then node and then left subtree.
  • For postorder , push the node, then the right subtree, and then left subtree.

Picture of stack at different times

image-20200904185344751

Level order Traversal

This strategy is based on reading top to down and left to right.

image-20200904194326643

Remarkably, we can achieve it just by changing one word in the last program.

exchanging stack by queue does it

because we process nodes in the order they appear.