2-Sorting Networks
Sorting Networks
Simplest model for studying nonadaptive sorting algorithms is an abstract machine that can access data only through compare-exchange operations. Such a machine is called a sorting network.
We draw network for N items as a sequence of N horizontal lines, with comparator connecting pairs of lines. We imagine keys to be sorted pass from right to left through the network, with a pair of numbers exchanged if necessary to put the smaller on top whenever a comparator is encountered.
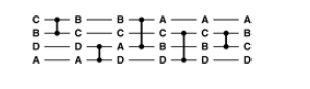
This network can sort any permutation of four keys.
A timing mechanism must be included to ensure that no comparator performs its operation before its input is ready.
Another important application of sorting networks is as a mode for parallel computation.
Given any network, it is not difficult to classify the comparators into a sequence of parallel stages that consists of groups of comparators that can operate simultaneously. For efficient parallel computation, our challenge is to design networks with as few parallel stages as possible.
Batcher Odd-Even Merging Network is one example. We can arrange it so that there is no interference.
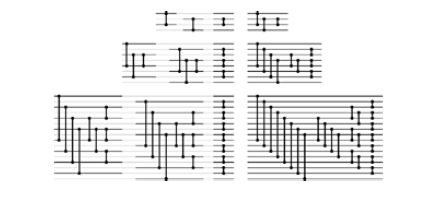
Batcher’s odd-even merge (non-recursive)
It accomplishes the merge in $\lg N$ passes consisting of uniform and independent compare-exchange instructions.
template <class Item>
void merge(Item a[], int l, int m, int r)
{ int N = r-l+1; // assuming N/2 is m-l+1
for(int k = N/2; k>0; k/=2)
for(int j=k%(N/2); j+k<N; j+=k+k)
for(int i=0; i<k; i++)
compexch(a[l+j+i],a[l+j+i+k]);
}
Property 3 : Batcher’s odd-even sorting networks have about $N(\lg N)^2 /4$ comparators and can run in $(\lg N)^2 /2$ parallel steps.
Batcher’s odd-even sort(non-recursive)
It divides into phases, indexed by variable p The last phase, when p is N, is Batcher’s Odd-even merge.
The next to last phase, when p is N/2 , is the odd-even merge with the first stage and all comparators that cross N/2 eliminated; the third to last-phase when p is N/4, is the odd-even merge with the first two stages and all comparators that cross any multiple of N/4 eliminated, and so forth.
template<class Item>
void batchersort(Item a[],int l, int r){
int N = r-l+1;
for(int p = 1; p<N; p+=p)
for(int k=p; k>0; k/=2)
for(int j=k%p; j+k<N; j+=(k+k))
for(int i=0; i<N-j-k; i++)
if((j+i)/(p+p) == (j+i+k)/(p+p))
compexch(a[l+j+i],a[l+j+i+k]);
}