5-Bottom up mergesort

Bottom-Up Mergesort

Bottom-Up mergesort

inline int min(int A, int B)
{return (A<B) ? A: B;}
template <class Item>
void mergesortBU(Item [a],int l, int r){
    for(int m = l; m <= r-l ; m = m+m )
        for(int i = l; i <= r-m; i+=m+m)
            merge(a,i,i+m-1,min(i+m+m-1,r));
}

Sequence of merges done by the recursive algorithm is determined by divide-and-conquer tree. We simply traverse tree in postorder or we can develop an alternate stack.

The only restriction is that files to be merged must have been sorted first.

For mergesort, it is convenient to do all the 1by1 merges first then all the 2by2 and so on.

This sequence corresponds to the level order traversal working up from the bottom of the recursion tree.

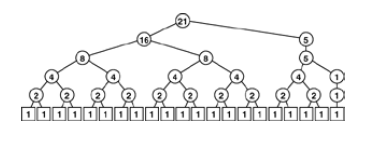
image-20201021164407381

  • All the merges in each pass of a bottom up mergesort involve file sizes that are a power of 2, except possibly the final file size
  • the number of passes in a bottom-up mergesort of N elements is precisely the number of bits in the binary representation of N ( ignoring leading 0 bits).

Key difference between Bottom-up merge sort it consist of series of series of passes through the file that merge together sorted sub files, until just one remains. Every element in the file, until just one remains.

While in top-down mergesort sorts the first half of the file before proceeding to the second half recursively, so progress is decidedly different.

image-20201021164919881