3-Algorithms on heap
Algorithms on Heap Data Structures
The PQ algorithms on heaps all work by first making a simple modification that could violate the heap condition and them traversing the and restoring the heap condition everywhere. This is known as Heapifying or fixing the heap.
There are 2 possibilities
- Priority of some node is increased : To fix it node should swim up the tree
- Priority of some node in decreased : To fix it node should swim down the tree
Lets say some node becomes larger than its parent then we can implement swim up using exchange operation on the both nodes and if problem is still (new parent is still smaller) not fixed we swap again.
Bottom-up Heapify (Swim-Up)
template <classs Item>
void fixUp( Item a[], int k){
while (k>1 && a[k/2] <a[k])
{ exch(a[k],a[k/2]); k=k/2;}
}
Lets say some node becomes smaller than both of its children nodes then we can swap it with the larger of its two children and proceed on doing the same until heap condition is satisfied.
Top-down Heapify (Swim-down)
template <class Item>
void fixDown( Item a[], int k , int N)
{
while (2*k <= N)
{
int j = 2*k;
if(j<N && a[j]<a[j+1]) j++; //To check whether we hit the bottom of heap
if(!(a[k]<a[j])) break; // this for condition is satisfied somewhere
exch(a[k],a[j]); k=j;
}
}
Heap based Priority Queue
//pq[0] is not used here :)
template <class Item>
class PQ
{
private:
Item *pq;
int N;
public:
PQ(int maxN)
{ pq = new Item[maxN+1]; N=0;}
int empty() const
{ return N==0; }
void insert(Item item){
pq[++N] = item; fixUp(pq,N);
}
Item getmax(){
exch(pq[1],pq[N]);
fixDown(pq,1,N-1);
return pq[N--];
}
};
Property 2 : The insert and remove the maximum operation for the priority queue abstract data type can be implemented with heap-ordered trees such that insert requires no more than $\lg N$ comparisons and remove the maximum no more than $2 \lg N$ comparisons, when performed on an $N$-item queue.
Inserting N items in the heap can at most take $N \lg N$ in worst case (if new each of new item is largest seen so far) But on average operation is linear time.
Example of heap construction: of keys A S O R T I N G
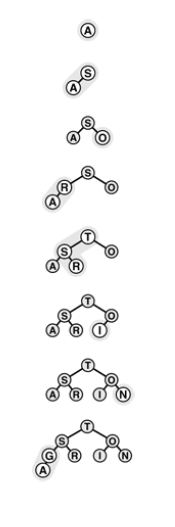
Property 3 : The change priority, remove, and replace the maximum operation for the priority queue abstract data type can be implemented with heap-ordered trees such that no more than $2 \lg N$ comparisons are required for any operation on an N-item queue.
Sorting with a priority queue
#include "PQ.cxx"
template <class Item>
void PQsort(Item a[], int l, int r){
int k;
PQ<item> pq(r-l+1);
for (k =l; k<=r ; k++) pq.insert(a[k]);
for (k = r; k>=l ; k--) a[k]=pq.getmax();
}
Time complexity of above sort is $\lg N + …+ \lg 2+\lg 1 $ which is $ < N \log N$