4-Heapsort
Heapsort
we can adapt idea of heap to sort an array without needing any extra space, by maintaining the heap within the array to be sorted.
we traverse from left to right using fixUp to ensure that the elements to the left are heap ordered complete tree. Then during the sortdown process, we put largest element into place vacated as heap shrinks.
SortDown is like selection sort but more efficient in finding largest item in unsorted array.
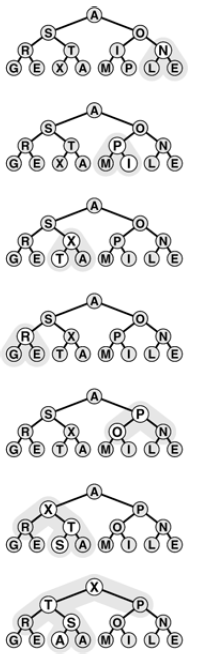
Rather than constructing the heap via successive insertions it is more efficient to build heap by going backward through it, making little subheaps from the bottom up.
Bottom up Heap construction
working from right to left and bottom to top, we construct a heap by ensuring that the subtree below the current node is heap ordered. Total cost is linear in worst case, because most nodes are near the bottom.
Full implementation is called as classical heap-sort algorithm
Property 4 : Bottom up heap construction takes linear time.
The for loop constructs heap, then the while loop exchange the largest element with the final element in the array and repairs the heap,continuing until the heap is empty. The pointer pq to a[l-1] allows the code to treat the subarray passed to it as an array with the first element at index 1, for the the array representation of complete tree.
template <class Item>
void heapsort(Item a[], int l , int r){
int k, N = r-l+1;
Item *pq = a+l-1;
for(k = N/2 ; k>= 1; k--)
fixDown(pq,k,N);
while(N>1)
{exch(pq[1],pq[N]);
fixDown(pq,1,--N);}
}
Property 5 : Heapsort uses fewer than $2N\lg N$ comparisons to sort $N$ elements.
(Inplace sorting algorithm)
Property 6 : Heap-based selection allows the Kth largest of N items to be found in time proportional to N when k is small or close to N, and in time proportional to N log N otherwise.
Improvements in Heapsort
-
Floyd : Note that an element is reinserted into the heap during the sortdown process usually goes all the way to the bottom, so we can save time by avoiding the check for whether the element reached its position, simply promoting the larger of two children until the bottom is reached,then moving back up the heap to the proper position.
This idea cuts comparisons by factor of 2 close to $\lg N $ ( absolute minimum comparisons for a sorting algorithm)
Quite useful where comparison operation is expensive like Long strings.
-
An array representation of heap-ordered ternary trees, with a node at positions 3k-1,3k,3k+1 and smaller than or equal to nodes at position at position at $\lfloor \frac{(k+1)}{3} \rfloor$.
This poses a trade off between decreasing tree height versus higher cost of finding largest children at each node.
**Dynamic Characteristics of heapsort **
left-construction of heap and right-sortdown process(exactly like selection sort)

The running time for heapsort is not particularly sensitive to the input. No matter what the input values are, the largest element is always found in less than $\lg N$ steps.
Which sort method to use :)
how to choose among heapsort,quicksort,and mergesort for a particular application.
The choice between heapsort and mergesort essentially reduces to a choice between stability and one uses extra memory.
Choice between heapsort and quicksort reduces to a choice between average case speed and worst case speed.
Its empirically proved that we can’t make heapsort faster than quicksort.