1-Glossary
Graph Properties and Types
Major Application of Graph includes Maps, Hypertext, Circuits, Schedules, Transactions, Matching, Networks, Program Structure(Compiler).
Glossary
Definition : A graph is a set of vertices and a set of edges that connect pairs of distinct vertices ( with at most one edge connecting any pair of vertices ).
We denote the number of vertices in a given graph by $V$ and number of edges by $E$.
Above definition puts two restrictions on graphs
- Disallow duplicate edges (Parallel edges, and a graph that contains them multigraph)
- Disallows edges that connect to itself (Self-Loops)
Property 1: A graph with $V$ vertices has at most $V(V-1)/2$ edges.
We use vertex when discussing graphs and nodes when discussing representation. We use edge when discussing graphs and links while discussing C++ data structures but mathematician/books might refer to mean same.
When there is a edge connecting two vertices, we say that the vertices are adjacent to one another and edges incident on it. The degree of vertex is number of edges incident on it. $v-w$ represents edge from $v$ to $w$ and $w-v$ represents edge from $w$ to $v$.
A subgraph is a subset of graph’s edges (and associated vertices) that constitutes a graph.
A drawing gives us intuition about the structure of graph but this intuition can be misleading, because graph is defined independently of the representation.
Same graph represented 3-ways
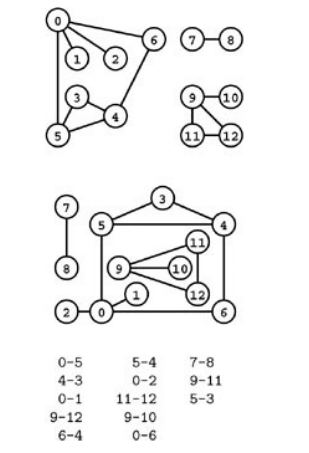
A graph is defined by its vertices and its edges, not the way that we choose to draw it.
A planar graph is one that can be drawn in the plane without any edges crossing. Figuring out whether a graph is planar or not is a fascinating problem itself. For some graphs drawing can carry information like vertices corresponding points on plane and distance represented by edges are called as Euclidean graphs.
Two graphs are isomorphic if we can change the vertex labels on one to make its set of edges identical to the other. (Difficult Computation Problem since there are $V!$ possibilities).
Definition : 2 A path in a graph is a sequence of vertices in which each successive vertex(after the first) is adjacent to its predecessor in the path. In a simple path, the vertices and edges are distinct. A cycle is a path that is simple except that the first and final vertices are the same.
Sometimes we refer cyclic paths to refer to a path whose first and last vertices are same; and we use term tour to refer to a cyclic path that includes every vertex.
Two simple paths are disjoint if they have non vertices in common other than, possibly, their endpoints.
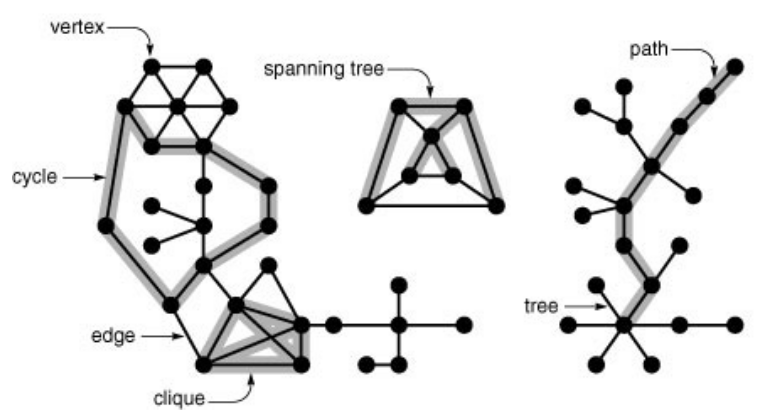
Definition 3: A graph is connected graph if there is a path from every vertex to every other vertex in the graph. A graph that is not connected consists of a set of connected components, which are maximal connected subgraphs.
Definition 4 : A acyclic connected graph is called a tree. A set of trees is called a forest. A spanning tree of a connected graph is a subgraph that contains all of that graph’s vertices and is a single tree.
A spanning forest of a graph is a subgraph that contains all of that graph’s vertices and is a forest.
A graph $G$ with $V$ vertices is a tree if and only if it satisfies any of the following four conditions.
- $G$ has $V-1$ edges and no cycles.
- $G$ has $V-1$ edges and is connected
- Exactly one simple path connects each pair of vertices in $G$
- $G$ is connected, but removing any edge disconnects it
Graphs with all edges present are called complete graphs.
Complement of a graph $G$ has same set of vertices as complete graph but removing the edges of $G$.
Total number of graphs with $V$ vertices is $2^{V(V-1)/2}$. A complete subgraph is called a clique.
density of graph is average vertex degree or $\frac{2E}{V}$. A dense graph is a graph whose density is proportional to $V$. A sparse graph is a graph whose complement is dense.
A graphs is dense if $E \propto V^2$ and sparse otherwise.
Density of graphs helps us choose a efficient algorithm for processing the graph.
When analysing graph algorithms, we assume $\frac V E$ is bounded above by a small constant, so we can abbreviate expression such as $V(V+E)\approx VE$.
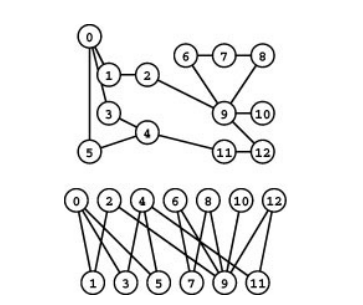
A bipartite graph is a graph whose vertices we can divide into two sets such that all edges connect a vertex in one set with a vertex in the other set. Its quite useful in matching problem. Any subgraph of bipartite graph is bipartite.
Graphs defined above are all undirected graphs. In directed graphs, also know as digraphs, edges are one-way. pair of vertices are in form of ordered pairs.
First vertex in digraph is called as source and final vertex is called as destination.
We speak of indegree and outdegree of a vertex ( the #edges where it is destination and #edges where it is source respectively)
A directed cycle in a digraph is a cycle in which all adjacent vertex pairs appear in the order indicated by (directed) graph edges
A directed acyclic graph (DAG) is digraph that has no directed cycles.
In weighted graphs we associate numbers (weights) with each edge, denoting cost or distance.