6-Comparisons and Improvemetns
Comparisons and Improvements
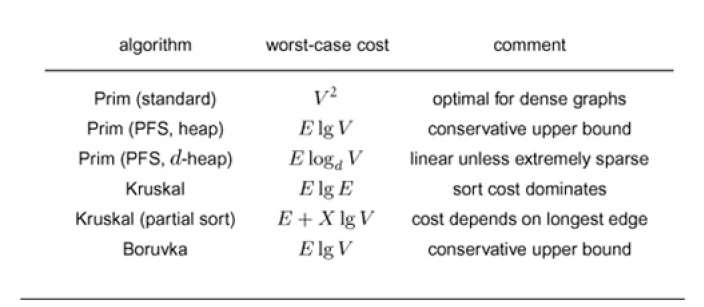
From the table we conclude adjacency-matrix implementation of Prim’s algorithm is method of choice for dense graphs, that all other methods perform within a small constant factor of best possible for graph of intermediate density, and that Kruskal’s method essentially reduces the problem to sorting for sparse graphs.
In short, we might consider the MST problem to be “solved” for practical purposes. FO most graphs, the cost of finding the MST is only slightly higher than the cost of extracting the graph’s edges.
First, much research has gone into developing better priority-queue implementation. The Fibonacci heap data structure, an extension of the binomial queue, achieves the theoretically optimal performance of taking constant time for decrease keys operation and logarithm time for remove the min operations, which behavior translates, to a running time proportional to $E+V\lg V$ for Prim’s algorithms.
One effective approach is to use radix methods for the priority-queue implementation. Performance of such methods is typically equivalent to that of radix sorting for Kruskal’s method, or even to that of using a radix quicksort for partial sorting method.
Another approach is proposed by D. Johnson in 1977 is one of the most effective. implement PQ for Prim’s algorithm with d-ary heaps.
Property 20.12 Given a graph with V vertices and E edges, let d denote the density E/V. If d <2, then the running time of Prim’s algorithm is proportional to V lg V. Otherwise, we can improve the worst-case running time by a factor of $\lg(E/V)$ by using a E/V-ary heap for the priority queue.