4-maxflow reductions
Maxflow Reductions
Maxflow in general networks Find the flow in a network that maximized the total outflow from its source ( and therefore total inflow to its sink). By convention flow is zero if there are no sinks or source.
Property 22.14 The maxflow problem for general networks is equivalent to the maxflow problem for st-networks.
Vertex Capacity constraints Given a flow network, find maxflow satisfying additional constraints specifying that the flow through each vertex must not exceed some fixed capacity.
Property 22.15 The maxflow problem for flow networks with capacity constraints on vertices is equivalent to the standard maxflow problem.
Acyclic Networks Find a maxflow in an acyclic network. Does the presence of cycles in a flow network make more difficult the task of computing a maxflow. ?
Property 22.16 The maxflow problem for acyclic networks is equivalent to the standard maxflow problem.
Maxflow in Undirected Networks
An undirected flow network is a weighted graph with integer edge weights that we interpret as capacities.
A circulation in such network is assignment of weights and direction to edges satisfying
- inflow = outflow at each vertex
- flow on each edge $\le$ capacity
Problem is to find a circulation that maximizes in a specific direction in a specific edge.
Property 22.17 The maxflow problem for undirected st-networks reduces to the maxflow problem for st-networks.
Feasible flow
-
Assign weights to vertex in flow network
-
Interpret as
- Supply ( >0 ),Demand ( < 0) under constraint $\Sigma w_{vertices} = 0 $
-
flow is feasible if $ V_{outflow}-V_{inflow} =wt_{V}$
Determine whether or not a feasible flow exists.
Property 22.18 The feasible-flow problem reduces to the maxflow problem.
Program 22.6 Feasible flow via reduction to maxflow
#include "MAXFLOW.cc"
template <class Graph, class Edge> class FEASIBLE {
const Graph &G;
void freeedges (const Graph &F, int v)
{
typename Graph::adjIterator A(F,v);
for(EDGE *e = A.beg(); !A.end(); e = A.nxt())
delete e;
}
public:
FEASIBLE(const Graph &G, vector<int> md) : G(G)
{
Graph F(G.V()+2);
for(int v = 0; v<G.V() ; v++)
{
typename Graph::adjIterator A(G,v);
for(EDGE *e = A.beg(); !A.end(); e = A.nxt())
F.insert(e);
}
int s = G.V(), t= G.V() +1;
for(int i = 0; i <G.V(); i++)
if(md[i] >= 0)
F.insert(new EDGE(s,i,md[i]));
else
F.insert(new EDGE(i,t,-md[i]));
MAXFLOW<Graph, Edge> (F,s,t);
freeedges(F,s); freeedges(F,t);
}
};
Maximum-cardinality bipartite matching Given a bipartite graph, find a set of edges of maximum cardinality such that each vertex is connected to at most one other vertex.
Property 22.19 The bipartite-matching problem reduces to the maxflow problem.
Corollary The time required to find a maximum-cardinality matching in a bipartite graph is $O(V E)$.
Program 22.7 Bipartite matching via reduction to maxflow
#include "GRAPHbasic.cc"
#include "MAXFLOW.cc"
int main(int argc, char *argv[]){
int s,t, N = atoi(argv[1]);
GRAPH<EDGE> G(2*N+2);
for(int i = 0; i<N; i++)
G.insert(new EDGE(2*N,i,1));
while(cin>>s>>t)
G.insert(new EDGE(s,t,1));
for(int i = N; i < 2*N; i++)
G.insert(new EDGE(i,2*N,2*N+1));
for(int i = 0; i < N ; i++)
{
GRAPH<EDGE>::adjIterator A(G,i);
for(EDGE* e = A.beg(); !A.end(); e = A.nxt())
if(e->flow() == 1 && e->flow(i))
cout<<e->v() << "-" << e-> w() << endl;
}
}
Next lets move on to connectivity in graphs.
Property 22.20 (Menger’s Theorem) The minimum number of edges whose removal disconnects two vertices in a digraph is equal to the maximum number of edge-disjoint paths between the two vertices.
Most important implication is mincut problem reduces to maxflow problem, but converse is not true.
Edge connectivity min no. of edges need to be removed to separate the graph into two pieces ? Find a set of edges of minimum cardinality that does this separation.
Vertex connectivity
Property 22.21 The time required to determine the edge connectivity of an undirected graph is $O(E^2)$
We consider a system of inequalities that involve one variable corresponding to each edge, two inequalities corresponding to each edge, and one equation corresponding to each vertex. The value of the variable is edge flow, the inequalities specify that the edge flow must be between 0 and the edge’s capacity, and the equations that specify that the total flow on the edges that go into each vertex must be equal to total flow on the edges that go out of that vertex.
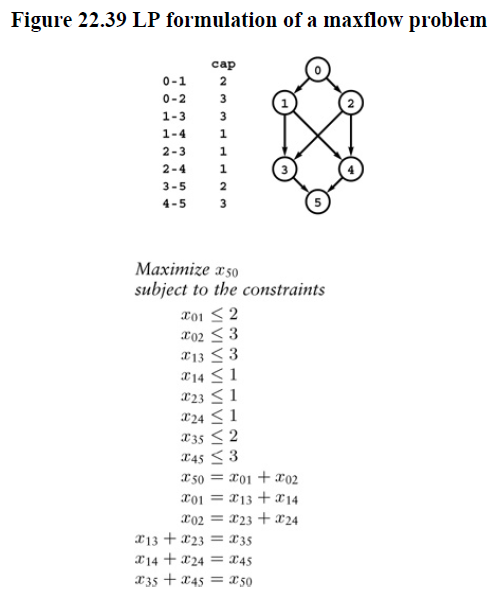
Any maxflow problem can be casted as a LP problem. LP is a versatile approach to solving combinatorial problems, and a great number of problems that we study can be formulated as linear programs.