DP 2

1D DP

Decode Ways :

Basically we see that the problem is a counting problem and we don’t want to enumerate.

Criteria for divide and conquer : lets find a criteria such that it makes solution mutually exclusive and exhaustive.

s1: set of all words made by considering only 1st character

s2: set of all words made by considering first 2 characters

Now lets try to connect to original subproblem.

Suffix Array :

Lets try to do the mathematical representation..

How many variables we require for suffix tree. => only one for starting index.

P <- f(S,0)

P1 <- f(S,1)

P2 <- f(S,2)

Recurrence : f(s,0) = f(s,1) + f(s,2);

f(s,1) : always counted because say 1034 we get 034 so its not valid split ( given ) we return 0

f(s,2) : not always counted if prefix > 26 even tho if we get positive answer.

or counted only if s[0…1] <= 26

Extra Step : Memoization

  1. check if DP problems by drawing tree.

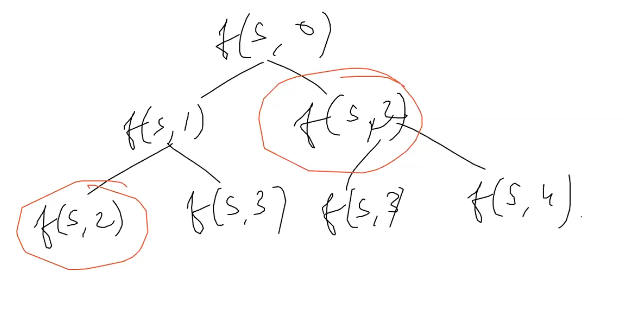
image-20210421190440244

  1. Design the storage -> size : n ( because n possible suffix array )

    ​ dimensionality : 1

Bottom Up solution

int numDecodings(string s) {
    int n = s.size();
    vector<int> dp(n);
    dp[n-1] = (s[n-1] == '0')?0 : 1;

    for(int i = n-2; i >= 0; i--){
        dp[i] = 0;
        // 2 cases
        // single digit
        if(s[i]!='0')
            dp[i]+=dp[i+1];

        // double digit
        if(s[i]=='1' || (s[i] == '2' && s[i+1] <= '6')){
            if(i == n-2)
                dp[i]+= 1;
            else 
                dp[i] += dp[i+2];
        }
    }
    return dp[0]; }

Simplified Code

int numDecodings(string s) {
    int n = s.size();
    vector<int> dp(n+1,0);
    dp[n] = 1;
    dp[n-1] = (s[n-1] == '0')?0 : 1;

    for(int i = n-2; i >= 0; i--){
        if(s[i]!='0')
            dp[i]+=dp[i+1];
        if(s[i]=='1' || (s[i] == '2' && s[i+1] <= '6'))
            dp[i] += dp[i+2];
    }
    return dp[0];
}

Best Time to Buy and Sell Stocks with Transaction Fee :

Cue : maximize profit ( try DP !)

DnC

  1. Criteria to split

For now we have seen Enumeration, Counting and now this is of type Maximize/Minimize.

We start out thinking with all possible txns.

so we can buy on 6th day and sell of 1st day ($b_6,s_1 $) like that there could be many element of the set. Now lets try to think of a criterial that gives us mutually exclusive and exhaustive sets.

So we buy on first day and don’t buy on first day.

  1. Lets try to relate the subproblem to original problem

    (Buy on 0th day)

    S_1 : max profit that you can make from D[1…n-1] , assuming the first thing you do is sell.

    [$S_i, (B_j S_k),(B_l S_m) … $]

    (Don’t buy on 0th day)

    S_2 : max profit that you can make from D[1…n-1] , assuming you start with a buy.

  2. Represent Subproblems Mathematically : degree of freedom we have is 2

    need 2 variables one is for suffix sum and second represent what we are doing whether a buy or sell operation. We can simply use a boolean for that representation.

    ​ D,1 ->D [1…(n-1)] // {selling first : 0}. // fee - constant

    S_1 : f (D, 1, 0 , fee)

    S_2 : f (D, 1, 1 ,fee)

    S : f (D, 0, 1 , fee)

    ​ buying can viewed as negative profit that is why D[0];

    f(D,0,1) = max(-D[0] + f(D,1,0) , f(D,1,1)) ….1

    wait but how u calculating f(D,1,0) there is no recurrence for it !

    this means we need one more recurrence

    f(D,0,0) = max(D[0] + f(D,1,1) - fee , f(D,1,0) ) …2

    sell - > 0 and buy ->1

    n(buy) : all suffix arrays

    n(sell) : all suffix arrays

Checking for DP , and its quite obvious from above relation we are repeating calls to function many times so it can be optimized using DP.

  1. Dimension - > 2
  2. Total -> 2*n

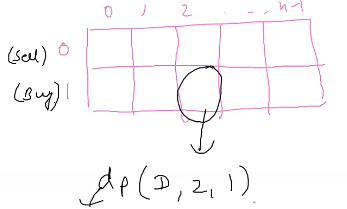
image-20210421213432998

dp(D,2,1) max. profit D[2…n-1] assume first buy

  • Filling the dp table can be complicated check the code

  • Base Cases ->

    dp(D,n-1,0) = D[n-1] - fee

    dp(D,n-1,1) = -D[n-1]

int maxProfit(vector<int>& prices, int fee) {
    int n = prices.size();
    vector<vector<int>> dp(n,vector<int>(2,0));
    // base case
    // 0-> sell
    // 1-> buy
    dp[n-1][0] = prices[n-1] - fee;
    dp[n-1][1] = max(0,-prices[n-1]);
    
    for(int i = n-2; i >= 0; i--){
        dp[i][0] = max(prices[i] - fee + dp[i+1][1] , dp[i+1][0]);
        dp[i][1] = max(dp[i+1][1], -prices[i]+dp[i+1][0]);
    }
    return dp[0][1]; }

Paint House :

There is a row of n houses where each house can be painted one of three colors: red, blue, or green. The cost of painting each house with a certain color is different. You have to paint all the houses such that no adjacent houses have the same color.

The cost of painting each house with certain color is represented by nx3 cost matrix

Return minimum cost to paint all houses.

( seems similar to house robber problem ) :

cue to recognize the DP , minimize the cost.

DnC -> criteria/decision ?

​ in a optimal solution house H1 can have either red,blue or color.

​ now try to find a way to divide them into sets such that they are mutually exclusive and mutually exhaustive.

  • S1 : H1 - > red , S2 : H1 -> green, , S3 : H1 -> blue

Defining the subproblem.

S1 : min cost to color H2…Hn st H2 != red

S2 : min cost to color H2…Hn st H2 != green

S3 : min cost to color H2…Hn st H2 != blue

Think of the way to represent the solution mathematically

P (H, i , C) -> min cost to color all house from H[i…n-1] such that Hi != C

P(H,i,C1) = min(cost[i][C2]+P(H,i+1,C2), cost[i][C3] + P(H,i+1,C3)) // 2 choices for the next house

Similarly P(H,i,C2) and P(H,i,C3)

Lets check whether we can use dp or not . Let’s draw a recurrence tree and you will observe that many repeated calls enable us to use DP

Design the table ? dimension = 2;

there are 2 dimension Suffix Array (n) and color (3)

so take nx3 array

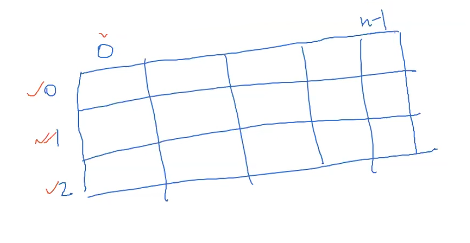
image-20210421230135228

dp(k,1) -> dp[K+1][0] and dp[k+1][2]

So this defines a order of populating the solution

Base Cases

dp[n][0...1] = 0

int minCost(vector<vector<int>>& costs){
    int n = costs.size();
    vector<vector<int>> dp(n+1,vector<int>(3,0));
    
    for(int i = n-1; i >= 0; i--){
  		dp[i][0]=min(costs[i][1]+dp[i+1][1],costs[i][2]+dp[i+1][2]);
        dp[i][1]=min(costs[i][0]+dp[i+1][0],costs[i][2]+dp[i+1][2]);
        dp[i][2]=min(costs[i][1]+dp[i+1][1],costs[i][0]+dp[i+1][0]);
    }
    return min(dp[0][0], min(dp[0][1] , dp[0][2]));
}

More compact representation , space wise make 2x3 size vector for solving it

Maximum Subarray

Find the subarray with maximum sum.

DnC

​ criteria : we wanna find out for every i -> max sum(s_i) subarray ending at i

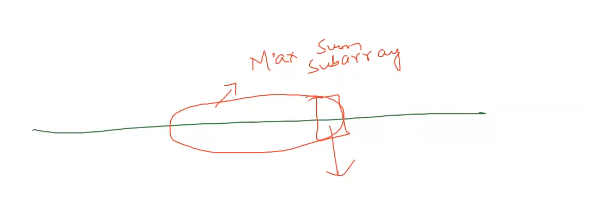
​ image-20210421235029931

​ res = max(s_i)

Step 2: compute S_i

​ Subarray ends at i`th element and it includes the A[i]

​ So there are 2 possibility

​ S_i = max { s_{i-1} + A[i] , A[i]};

DP : yes , 1D table and its prefix array

dp[i] = s_i

Base Case : dp[0] = nums[0]; // taken care while declaring the dp vector we explicitly set it to zero

int maxSubArray(vector<int>& nums) {
    int n = nums.size(),i,res = INT_MIN;
    vector<int> dp(n+1,0);

    for(i = 1; i <= n; i++){
        dp[i] = max(dp[i-1]+nums[i-1] ,nums[i-1]);
        res = max(res,dp[i]);
    }     return res; }

We can do it 2 size vector or 2 variable

Kadane’s Algorithm

int maxSubArray(vector<int>& nums) {
    int n = nums.size(),i,res = INT_MIN;
	int prev = 0, curr;
    for(i = 1; i <= n; i++){
        curr = max(prev+nums[i-1] ,nums[i-1]);
        res = max(res,curr);
        prev = curr;
    } return res; }

Maximum Product Subarray

P_i <= max product sub. ending at i

ans = max{P_i}

P_i : max(P_i-1*A[i] , A[i])

P_i’ Min Product sub array ending at i-1

P_i’ : max(P_i ’ *A[i] , A[i])

Base Case -> dp[0] = nums[0] for both min / max function

int maxProduct(vector<int>& nums) {
    int n = nums.size(),i, res = INT_MIN;
    vector<int> minProd(n+1,1);
    vector<int> maxProd(n+1,1);

    for(i = 1; i <= n; i++){
        minProd[i] = min(nums[i-1], min(nums[i-1]*minProd[i-1],nums[i-1]*maxProd[i-1]));
        maxProd[i] = max(nums[i-1], max(nums[i-1]*minProd[i-1],nums[i-1]*maxProd[i-1]));
        res = max(res,maxProd[i]);

    } 
    return res; }

Largest Valid Parenthesis : easily can be done using stack.

Using the Kadane Algorithm

Assume s_i : represents the longest valid parentheses ending at i.

res = max {s_i} for all i : 0…n-1

s_i = 0 if A[i] = “(”

now case of “)” we see that $s_{i-1}$ in closed somewhere and we go backwards at a index $j$ that is opening parenthesis before the solution $s_{i-1}$

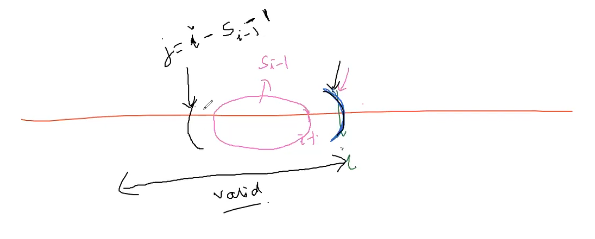
image-20210422081002163

There are two possibilities A[j] = “)” then this is done you can’t find the longest from the solution of $s_{i-1}$. otherwise increment the longest pair.

$$ \begin{equation} S_{i} = \begin{cases} 0 & \text{if } A[i] &= “(” \ 0 & \text{if } A[i] &= “)” \ 2+s_{i-1} + s_{j-1} & \text{if } A[j] &= “)”\ \end{cases}
\end{equation} $$

Here $ j = i - s_{i-j} -1$

int longestValidParentheses(string s) {
    int n = s.size(),i,j,res = 0;
    vector<int> dp(n);
    
    for(int i = 1; i < n; i++){
        if(s[i] == '(')
            dp[i] = 0;
        else{
            j = i - dp[i-1]-1;
            if(j >= 0 && s[j] == '('){
                dp[i] = 2+dp[i-1];
                if(j-1 >= 0)
                    dp[i]+= dp[j-1];
            }
        }
        res = max(res,dp[i]);
    }    return res; }

We can optimize the code size :) use zero initialized indices, saves of many checks.