DP 4
2D DP
Target Sum
Cue : DP/DnC , as there is counting problem.
Let’s decide the criteria of splitting the set
Splitting the set into 2 components , set s1 contains sum with A[0] in positive sign
another set s2 with A[0] in negative sign.
$S_1 $ : Number of ways to make target-A[0] from A[1,… n-1]
$S_2 $ : Number of ways to make target+A[0] from A[1,… n-1]
Mathematical Representation of problem
P(A,i , target)
Recurrence : P(A,0,target) = P(A,1,target-A[0]) + P(A,1,target+A[0])
Justify use of DP : +2 , -2 , … => P(A,2, target)
-2 , +2, … => P(A,2, target)
So overlapping subproblem.
Design Table : Dimensions ? -> 2D - > suffix array , target
Size : $n\times (2+(\Sigma A[i]+1))$
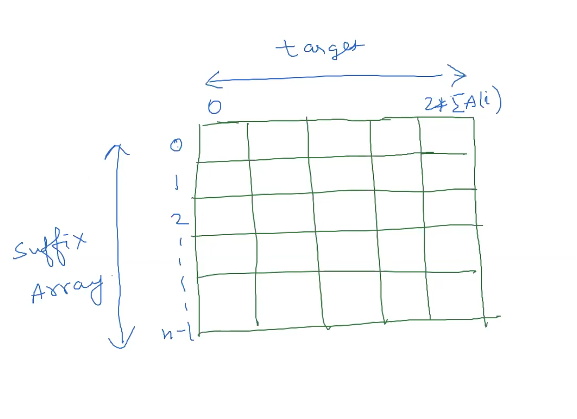
Order of traversal : Simulate the recurrence on the table.
Bottom of table to up . no constraint on movement in table ( lets say go to L to R)
Base Case : n-1 row where the 1 where target == A[n-1] otherwise 0 , or using n
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size(), i, j;
vector<vector<int>> dp(n+1, vector<int> (2001,0));
// sum = 0
// -1000 to 1000 => [0,2000]
// 0 to 1000
dp[n][1000] = 1;
for(i = n-1; i >= 0; i--){
for( j = -1000; j <= 1000; j++){
// two cases
// +ve sign
if(j+1000-nums[i] >= 0)
dp[i][j+1000] += dp[i+1][j+1000-nums[i]];
// -ve sign
if(j+1000+nums[i] <= 2000)
dp[i][j+1000] += dp[i+1][j+1000+nums[i]];
}
} return dp[0][target+1000]; }
We can optimize further with 2x(2001) size array
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size(), i, j;
vector<vector<int>> dp(2, vector<int> (2001,0));
// sum = 0
// -1000 to 1000 => [0,2000]
// 0 to 1000
dp[n%2][1000] = 1;
for(i = n-1; i >= 0; i--){
for( j = -1000; j <= 1000; j++){
dp[i%2][j+1000] = 0;
// two cases
// +ve sign
if(j+1000-nums[i] >= 0)
dp[i%2][j+1000] += dp[(i+1)%2][j+1000-nums[i]];
// -ve sign
if(j+1000+nums[i] <= 2000)
dp[i%2][j+1000] += dp[(i+1)%2][j+1000+nums[i]];
}
} return dp[0][target+1000]; }
line 15 and 19 have a bug that dp[x%2] += dp[(x+1)%2] expands to dp[x%2] = dp[x%2]+dp[(x+1)%2]
So we change the x%2 row while performing on it.
But we fixed it with line 11 trick.
Coin Change
Very famous and standard problem.
We does greedy fails : moving from larger denomination to lower denominations.
taking off larger denomination doesn’t mean that it decreases the number of denomination required to make the sum.
[ 1, 15, 25] => get total 30
greedy says 1-> 25 and 5->1 coins : 6
while optimal is 2->15 coins : 2
Lets decide set : all possible combination to get the sum and we need to divide the set.
Criteria : $s_1 $ : contains zero($=0$) denomination of first coin
$s_2 $ : contains more than zero($> 0$) denomination of first coin
Subproblem : s_1 : find the given sum excluding first coin : A[1…n-1]
s_2 : make (sum - A[0]) using the A[0…n-1]
P(A,0,target) = min {P(A,1,target) , 1+P(A,0,target-A[0])}
DP : overlapping subproblem.
2 D one dimension sum and suffix array
size n*(target+1)
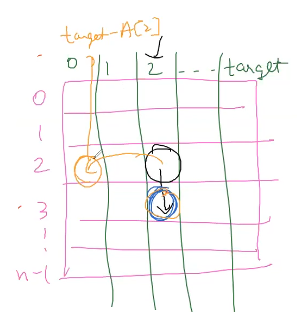
order of filling : we see we need bottom row and and a column somewhere behind the current element.
bottom to top and left to right
Base Case : n row make dp[n][0] = 0 dp[n][1...target] = INT_MAX // because we are taking min in each step so INT_MAX will be replaced eventually with some minimum.
int coinChange(vector<int>& coins, int amount) {
int n = coins.size(), i, j;
vector<vector<int>> dp(n+1, vector<int>(amount+1,INT_MAX));
dp[n][0] = 0;
for(i = n-1; i>= 0; i--){
for(j = 0; j <= amount; j++){
dp[i][j] = dp[i+1][j];
if(j-coins[i] >= 0 && dp[i][j-coins[i]] != INT_MAX)
dp[i][j] = min(dp[i][j], 1+dp[i][j-coins[i]]);
}
} return dp[0][amount] == INT_MAX ? -1: dp[0][amount];}
Space Optimized Solution
int coinChange(vector<int>& coins, int amount) {
int n = coins.size(), i, j;
vector<vector<int>> dp(2, vector<int>(amount+1,INT_MAX));
dp[n%2][0] = 0;
for(i = n-1; i>= 0; i--){
for(j = 0; j <= amount; j++){
dp[i%2][j] = dp[(i+1)%2][j];
if(j-coins[i] >= 0 && dp[i%2][j-coins[i]] != INT_MAX)
dp[i%2][j] = min(dp[i%2][j], 1+dp[i%2][j-coins[i]]);
}
} return dp[0][amount] == INT_MAX ? -1: dp[0][amount];}
Follow up you can optimize with 1 row , :) hint : see line 8 as we are not touching anything beyond dp[i] while populating it thats why everything that we were storing below can be maintained in same array after dp[i] and voila !
int coinChange(vector<int>& coins, int amount) {
int n = coins.size(), i, j;
vector<int> dp(amount+1,INT_MAX);
dp[0] = 0;
for(i = n-1; i>= 0; i--)
for(j = 0; j <= amount; j++)
if(j-coins[i] >= 0 && dp[j-coins[i]] != INT_MAX)
dp[j] = min(dp[j], 1+dp[j-coins[i]]);
return dp[amount] == INT_MAX ? -1: dp[amount];}
Follow up :
Try solving the problem using the following criteria
s1 : picking 1st coin and finding solution
s2 : picking 2nd coin and finding solution
s3 : ""
…
s_n :
Recurrence
P(target) = 1+min$_{0\le i\le n} ${P(target-A[i])}
Dimension of this DP : 1D
0 to target size table
order of filling : 0 to target.
Base Case : dp[0] = 0 and fill rest of it with dp[1...n-1] = INT_MAX
but There is a catch : it will count 1 , 2 , 1 and 2, 1, 1 as different
so it counts duplicates xD.
These Coin Change problems are Knapsack Problem ( Integer Knapsack )
Integer Knapsack
Similar to coin change we have to take items such that we get maximum value and capacity less that max capacity while filling up the knapsack
Items : $I_1 \ I_2 … I_n $
Value : $v_1 \ v_2 … v_n $
Capacity : $c_1 \ c_2 … c_n $
Criteria : Solving the problem based on whether we get maximum capacity by including and not including first element in set
Subproblems :
$S_1 $ : solving knapsack including the Item-1
$S_2 $ : solving knapsack without the Item - 2
P(A,i,cap) = max { $v_i $ + P(A,i+1,cap-$c_i $) , P(A,i+1, cap) }
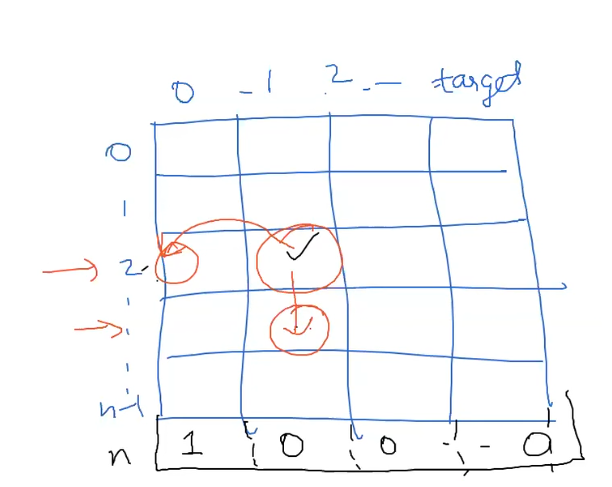
This shows order of filling the table.
Fractional Knapsack
Here we are allowed to take items partially
we have Items : we can take fractional capacities and fractional values according to it. Its not DP problem anymore. rather calculate capacity / value and try to optimize it greedily.
2D DP with both dimensions suffix/prefix arrays.
Very widely used problem and i got it for interview once :)
Edit Distance
Minimum numbers of transforms for converting string s_1 into s_2
There are 3 operation : insert, delete and replace.
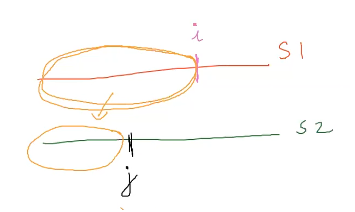
Here we can say dp[i][j] refers to minimum operation needed to convert s1[0….i] to s2[0….j].
dp[i][j] = dp[i-1][j-1] if s1[i] == s2[j];
if s1[i]!=s2[j]
dp[i][j] = dp[i-1][j-1]+1 : replace operation
dp[i][j] = dp[i][j-1]+1 : insertion operation
dp[i][j] = dp[i-1][j]+1 : delete operation
dp[i][j] is minimum of above operation.
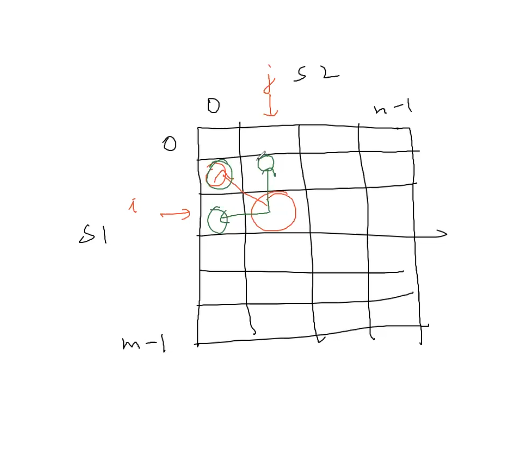
order of filling from top to down and left to right
Base Case : to transform [a] into [ab….] if there is a in second word then $n-1$ deletion otherwise $n$. Simpler base case is by shifting everything by one. :)
we add a row above the table and column of left side too. just to make the base case simpler.
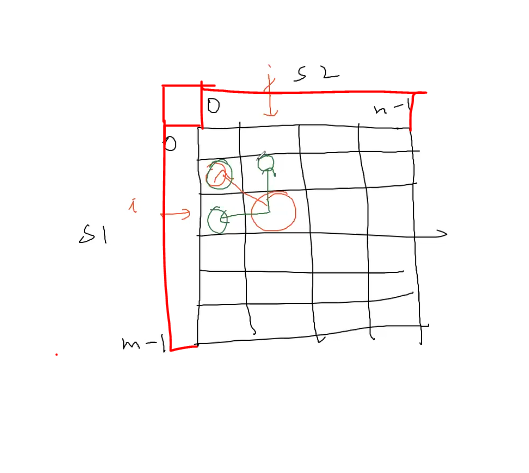
Now for s1 : [" “, “a” , “ab” , … ] transform to [”"]
see 0 , 1 , 2, 3 , 4, … delete operation // filling in extra column
Now for s1 : [""] transform to [" “, “a " , “ab” , ….]
see 0,1,2,3,4, … insert operation // filling the extra row we took.
int minDistance(string word1, string word2) {
int m = word1.length(),n = word2.length(),i,j;
vector<vector<int>> dp(m+1, vector<int> (n+1,0));
// base cases
for(i = 0 ; i <= n ; i++) dp[0][i] = i;
for(j = 0 ; j <= m ; j++) dp[j][0] = j;
// actual DP implemenation
for(int i = 1 ; i <= m ; i++)
for(int j = 1 ; j<= n ; j++)
if(word1[i-1] == word2[j-1])
dp[i][j] = dp[i-1][j-1];
else
dp[i][j] = 1 + min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]});
return dp[m][n]; }
Space state optimization
we need 2 rows only to give answer to the problem.
int minDistance(string word1, string word2) {
int m = word1.length(),n = word2.length(),i,j;
vector<vector<int>> dp(2, vector<int> (n+1,0));
// base cases
for(i = 0 ; i <= n ; i++) dp[0][i] = i;
// actual DP implemenation
for(int i = 1 ; i <= m ; i++){
dp[i%2][0] = i;
for(int j = 1 ; j<= n ; j++)
if(word1[i-1] == word2[j-1])
dp[i%2][j] = dp[(i-1)%2][j-1];
else
dp[i%2][j] = 1 + min({dp[(i-1)%2][j], dp[i%2][j-1], dp[(i-1)%2][j-1]});
} return dp[m%2][n]; }
Distinct Subsequences
dp[i][j] : # number subsequences of s1 [0…i] in s2[0…j]
two cases now :
if same characters s1[i] == s2[j] then
dp[i][j] =dp[i-1][j-1]+dp[i-1][j]
otherwise
dp[i][j] = dp[i-1][j]
Dp will go from top to down, left to right
left to right -> 2 rows and right to left ->1 row (think!)
extra row and columns to simplify the Base Case
int numDistinct(string s, string t) {
int m = s.size(),n = t.size(), i, j;
vector<vector<unsigned long>> dp(m+1,vector<unsigned long>(n+1,0));
// fill the first colums with 1s
for(i = 0; i <= m; i++) dp[i][0] =1;
for(i = 1; i<=m ; i++){
for(j = 1; j<=n; j++){
dp[i][j] = dp[i-1][j];
if(s[i-1]== t[j-1])
dp[i][j]+= dp[i-1][j-1];
}
} return dp[m][n]; }
Long long dp table required because of constraints !
using 1 Dimension DP : // reason if we observe while filling dp[i][j] right to left we need the values before the dp[i][j] cell and thats why we can store the result of processing dp[i][j] onto the same row as we are not disturbing the trailing cells.
int numDistinct(string s, string t) {
int m = s.size(),n = t.size(), i, j ,temp;
vector<unsigned long> dp(n+1,0);
dp[0] = 1;
for(i = 1; i<=m ; i++)
for(j = n; j>=1; j--)
if(s[i-1]== t[j-1])
dp[j]+= dp[j-1];
return dp[n]; }