DP 5
2D DP : Subproblem -> Subarray
Stone Game
Game’s Outcome is Deterministic !
We can simply see because of the constraint of the game that both plays optimally and alex can lock a particular indices ( odd/ even) as she is always beginning the game. As a result she knows which index to choose(odd/even) that has more sum. So we can conclude alex wins always!
return true; ;)
method 2
DnC
Let’s say set is composed of all possible combinations alex wins and now lets split them into mutually exclusive and exhaustive set. We can split them on the basis of whether she pick A[0] , A[1] , … A[n-1]
Original Problem : Alex goes first whether Alex wins/loss given A[0…n-1]
subsets : lee goes first and whether Alex wins/loss given A[1…n-1]
in case Alex chooses A[n-1] then second config becomes lee goes first and whether Alex wins/loss given A[0…n-2].
There are 3 dimensions to DP
Nature of Subproblem : general subarray
2D subproblem
Representation of Problem
P1(A,i,j) - Assuming Alex goes first
P2(A i,j) - Assuming Lee goes first
Actual problem Will Alex win if P1 or P2
P1 (A,i,j) = P2(A,i+1,j) || P2(A,i,j-1)
Problem statement needs to expanded as we need score to decide who wins
P1(A,i,j) <- Alex - lee score for A[i….j] Assuming Alex goes first
P2(A,i,j) <- Alex - lee score for A[i…j] Assuming lee goes first
P1(A,i,j) = max {A[i] + p2(A,i+1,j) , A[j] + p2(A,i,j-1) }
P2(A,i,j) = max { p1(A,i+1,j)-A[i] , p(A,i,j+1)-A[j] }
P(A,i,j) : whoever is going first <- max(S_1 - S_2);
Difference between scores of P1 and P2 assuming P1 goes first.
P(A,i,j) = max {A[i] - P(A,i+1,j) , A[j] - P(A,i,j-1) }
Repeated subproblems
DP table -> order of filling.
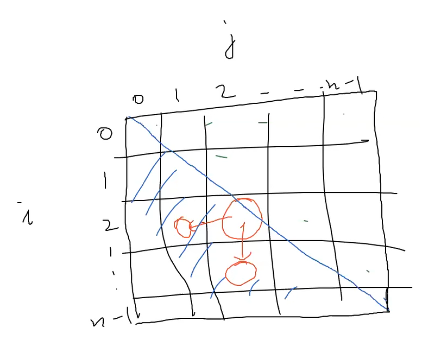
we can see the order is top to up and left to right and since i <= j , we are just using the lower triangular matrix.
we can fill the principle diagonal before using i = j we can do A[i]
Now there is no issue of out of bound indices.
bool stoneGame(vector<int>& piles) {
int n = piles.size(), i, j;
vector<vector<int>> dp(n,vector<int>(n,0));
// diagonal
for(i = 0; i <n ; i++) dp[i][j] = piles[i];
for(i = n-2; i >= 0; i--)
for( j = i+1; j <n; j++)
dp[i][j] = max(piles[i]-dp[i+1][j],
piles[j] - dp[i][j-1]);
return dp[0][n-1] > 0; }
Can we do better.
hmm we can fill it diagonally :)
Longest Palindromic Subsequence
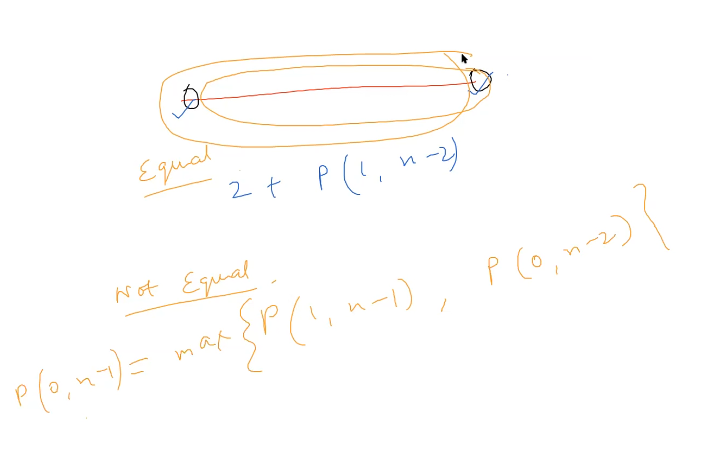
Exactly same as previous question!
int longestPalindromeSubseq(string s) {
int n = s.size(), len, i;
vector<vector<int>> dp(n,vector<int>(n,0));
// length wise
for(len = 1; len <= n; len++)
for(i = 0; i+len-1 < n; i++)
if(len == 1)
dp[i][i] = 1;
else {
// s[i][i+len-1]
if(s[i] == s[i+len-1])
dp[i][i+len-1] = 2+(i+1> i+len-2?0:dp[i+1][i+len-2]);
else
dp[i][i+len-1] = max(dp[i+1][i+len-1],dp[i][i+len-2]);
} return dp[0][n-1]; }
Burst Balloons
There is a definite order that yields maximum sum that order is one of all the permutations of bursting the balloon.
Set : all permutations or order of bursting of balloon
Subproblem : s1 : the permutation in which balloon B1 is burst at the end
similarly for s2, s3, …. sn
Now we didn’t burst in middle because that will cause us to have knowledge of all balloons bursting on right and left for answering the query further, they are not independent. But picking up last balloon makes us sure that balloons only exists in left side.
Say we burst Bi last
then solution becomes (B0 …. B{i-1}) + (B{j+1} …. B{n-1}) + 1 * B_i * 1
$ dp(i,j) = max_{i\le k\le j}{ dp(i,k-1) + dp(k-1,j) + A[k]} $
Solution is $O(n^3)$
int maxCoins(vector<int>& nums) {
int n = nums.size(), len, i, k, left=1, right=1, left_term, right_term;
vector<vector<int>> dp(n,vector<int> (n,0));
// dp
for(len = 1; len <= n; len++){
for(i = 0; i+len-1 < n; i++){
// nums[i][i+len-1]
for(k = i; k <= i+len-1; k++){
left = right = 1;
if(i-1 >= 0) left = nums[i-1];
if(i+len-1+1 < n) right = nums[i+len-1+1];
left_term = right_term = 0;
if(k-1 >= 0) left_term = dp[i][k-1];
if(k+1 < n) right_term = dp[k+1][i+len-1];
dp[i][i+len-1] = max(dp[i][i+len-1],
left_term+right_term+
left*nums[k]*right);
}
}
} return dp[0][n-1]; }
Matrix DP
Input in single array
1D DP
- integer
- suffix / prefix Array
2D DP
- integers, suffix/prefix
- 2 suffix/prefix
- subarrays
Now we have matrix DP, given matrix as input
Minimum Path Sum
(0,0) to (m-1,n-1)
constraint : down and right movement only
finding the path with least sum.
Minimize sum
DnC
Lets all paths be a set that we will try to split. Split the set into mutually exclusive and exhaustive subsets.
Two sets : on the basis of first step in path , i.e. first step right or first step down
Lets define subproblems
S1 : Min. path sum given that first step is right step of matrix with top left corner as (1,0) and bottom right corner (m-1,n-1)
S2 : Min. path sum given that first step is down step of matrix with top left corner as (0,1) and bottom right corner (m-1,n-1)
All matrices are suffix matrix of the original matrix.
Recurrence
p(x,y) <= min. sum path of matrix with top left corner as (x,y) as right bottom corner as (m-1,n-1)
P(0,0) <= Original Problem
P(0,0) = min {P(0,1) , P(1,0)} + A[0][0]
can we use DP ? yes overlapping subproblems
Dimensions : 2
Size : mxn
Base Cases : declare extra row and column in the end and make that value INT_MAX
or default table : for last row and column its just the sum of path travelled.
Order of Filling : (simulate the recurrence on the table) Fill from the bottom to top and right to left
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size() ,i ,j ;
vector< vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
dp[m][n-1] = dp[m-1][n] = 0;
// bottom to top , R to L
for(i = m-1; i>=0; i--)
for(j = n-1; j>=0; j--)
dp[i][j] = grid[i][j] + min(dp[i+1][j],dp[i][j+1]);
return dp[0][0]; }
Space State Optimization ? xD
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size() ,i ,j ;
vector<int> dp(n+1,INT_MAX);
dp[n-1] = 0;
// bottom to top , R to L
for(i = m-1; i>=0; i--)
for(j = n-1; j>=0; j--)
dp[j] = grid[i][j] + min(dp[j+1],dp[j]);
return dp[0]; }
Dungeon Game
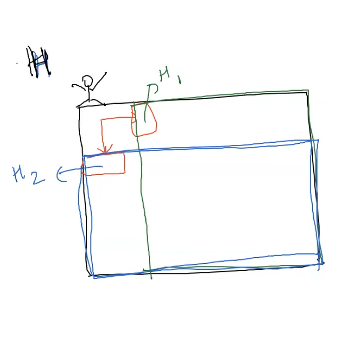
H_1 <= Initial min. health of knight for rescuing in the box (0,1) to (m-1,n-1)
H_2 <= Initial min. health of knight for rescuing in the box (1,0) to (m-1,n-1)
By definition H1 > 0 and H2 > 0
dp[0][0] = val
so say H_1 is -6 and H_2 is -5 so we can think solving the subproblem with initial health val - 6 or val -5 and its guaranteed that one path will lead to solution by problem constraint.
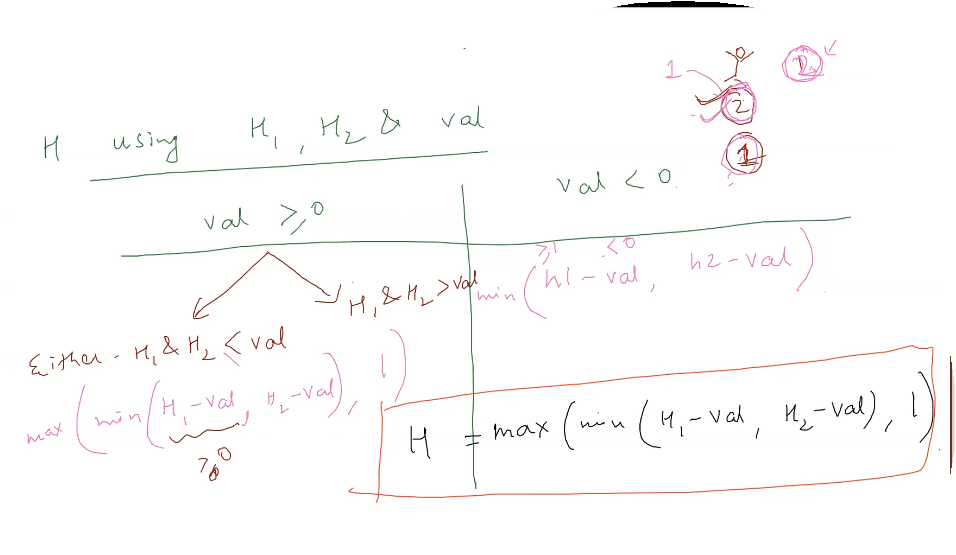
Base Case :
bottom row : $ H_1 = max(H_1-val , 1)$
right column : $H2 = max(H_2 - val,1)$
Order of filling : B to T and R to L
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int m = dungeon.size(), n = dungeon[0].size(), i , j;
vector<vector<int>> dp(m,vector<int> (n,INT_MAX));
dp[m-1][n-1] = max(1-dungeon[m-1][n-1],1);
for( i = m-1; i >= 0; i--){
for(j = n-1; j >= 0; j--){
if(i+1 < m)
dp[i][j] = min(dp[i][j],
dp[i+1][j] - dungeon[i][j]);
if(j+1 < n)
dp[i][j] = min(dp[i][j],
dp[i][j+1] - dungeon[i][j]);
dp[i][j] = max(1,dp[i][j]);
}
} return dp[0][0];}
Frog Jump
Split criteria : at each step there are 3 possibilties of jumping k , k+1 , k-1
Dp(S_i) (k) <- can u reach the last stone starting from s_i assuming the last just made was k.
dp($S_i$)(k) = dp($s_j$)(k-1) || dp($s_l $)(k) || dp($s_m$)(k+1)
$s_j = s_i + k-1, s_l = s_i+k, s_m = s_i + k + 1 $
s represents the indices
DP Table : 2D table
size : n x n
( max possible jump is n+1)
Order of filling : bottom to top
bool canCross(vector<int>& stones) {
if(stones[1]!=1)
return false;
int n = stones.size(), i ,j;
unordered_map<int,int> m;
vector<vector<bool>> dp(n,vector<bool>(n+1,false));
// populate the map
for(i = 0; i <n; i++){
m[stones[i]] = i;
dp[n-1][i+1] = true;
}
// DP table
for(i = n-2; i >= 1; i--){
for(j = 1; j <= n; j++){
// 3 casese
if(j > 1 && m.find(stones[i]+j-1) != m.end())
dp[i][j] = dp[i][j] || dp[m[stones[i]+j-1]][j-1];
// j
if(m.find(stones[i]+j) != m.end())
dp[i][j] = dp[i][j] || dp[m[stones[i]+j]][j];
// j+1
if(m.find(stones[i]+j+1) != m.end())
dp[i][j] = dp[i][j] || dp[m[stones[i]+j+1]][j+1];
}
} return dp[1][1]; }
Above solution gives a TLE :)
for all the k stones we don’t need to store last possible sum
we need only few k values :
Bottom up -> always computing all subproblems
Top Down solution computes only the needed subproblem
Now if we do Top to Down solution this should not give TLE
bool canCrossHelper(unordered_map<int,int>& m, vector<vector<int>> &dp ,int i, int j , vector<int>& stones){
int n = stones.size();
// base case
if( i == n-1) return true;
// dp step
if(dp[i][j]!= -1) return dp[i][j];
int t1 = 0, t2=0, t3 = 0;
// 3 casese
if(j > 1 && m.find(stones[i]+j-1) != m.end())
t1 = canCrossHelper(m,dp,m[stones[i]+j-1],j-1,stones);
// j
if(m.find(stones[i]+j) != m.end())
t2 = canCrossHelper(m,dp,m[stones[i]+j],j,stones);
// j+1
if(m.find(stones[i]+j+1) != m.end())
t3 = canCrossHelper(m,dp,m[stones[i]+j+1],j+1,stones);
dp[i][j] = t1 || t2 || t3;
return dp[i][j];
}
bool canCross(vector<int>& stones) {
if(stones[1]!=1)
return false;
int n = stones.size(), i ,j;
unordered_map<int,int> m;
vector<vector<int>> dp(n,vector<int>(n+1,-1));
// populate the map
for(i = 0; i <n; i++){
m[stones[i]] = i;
} return canCrossHelper(m,dp,1,1,stones);}
| Top - Down | Bottom-Up |
|---|---|
| No space optimizations | Space Optimization |
| Recursive call-stack overheads + stack overflow | Simple Iterative |
| Doesn’t comput all subproblmes ( time optimization) | Computes all states/subproblems |