> Problems : Graphs > Graphs 3

Graphs 3

Shortest Paths in Weighted Graph

Weighted Graphs quantify degree of relationship between vertices.

This weight is on edges.

Earlier during level traversal we used to queue to get most recent insertion but now we will use priority queues. Now last in last out property now will be on the basis of weights.

Network Delay Time

Problem is correctly solved using MSTs

But we will solve using above concept.

int networkDelayTime(vector<vector<int>>& times, int n, int k) {
    // construct the graph.
    vector< vector<pair<int, int>>> graph(n+1);
    vector<bool> visited(n+1, false);
    int res = 0, count = 0;

    for(const auto& edge : times){
        graph[edge[0]].push_back({edge[2],edge[1]});
    }

    // weighted BFS.
    // Declare a min Priority Queue.
    // second argument decides the implementation of PQ
    priority_queue<pair<int,int>,/* internal implementation */
        vector<pair<int,int>>,/* Type of priority */ greater<pair<int,int>> > pq;

    pq.push({0,k});

    while(!pq.empty()){
        pair<int, int> t = pq.top();
        pq.pop();

        if(visited[t.second])
            continue;

        visited[t.second] = true;
        count++;
        
        // shortest path from k to t.second
        res = max(res, t.first);

        // push all the nbrs.
        for(const auto& nbrs: graph[t.second]) {
            if(!visited[nbrs.second])
            	pq.push({t.first+nbrs.first, nbrs.second});
        }
    }
    return count == n ? res : -1;
}

This is Dijkstra’s Algorithm

Before moving on lets review what we have practiced so far!

Graph
Connectivity
Cyclicity
- Topological Sort
Shortest Path

Shortest Path

Unweighted graph : level order traversal (BFS)
Weighted graph : weighted BFS

Path with Maximum Minimum Value

Given matrix of integers A with R rows and C columns. Finding the maximum score of a path starting at [0,0] and ending at [R-1, C-1].

The score of a path is the minimum value in that path. So basically look for the path which has largest minimum value.

Its more like longest paths cause we need maximum score.

Now if there is cycle then longest path is not defined. We can utilize the DP concept here. $p_j$ = max($e_i$ + $p_i$)

Remember cyclic dependency hurts DP at its core! :) We get in dilemma for example.

$A$ requires us to solve a subproblem that is $B$ but after few calculation for you see that solving $B$ requires solving $A$. Its like a snake eating its tail!

vector<vector<int>> dirs = {{0,1},{1,0},{-1,0}, {0,-1}};
int maximumMinimumPath(vector<vector<int>>& A) {
    int m = A.size(), n = A[0].size(), i, j;
    priority_queue<vector<int> , vector<vector<int>>,
    	less<vector<int>> > pq;
    vector<vector<bool>> visited(m,vector<bool>(n,false));
    
    pq.push({A[0][0],0,0});
    
    while(!pq.empty()) {
        vector<int> t = pq.top();
        pq.pop();
        
        if(visited[t[1]][t[2]])
            continue;
        visited[t[1]][t[2]] = true;
        
        if(t[1] == m-1 && t[2] == n-1 )
            return t[0];
        // traverse the nbrs
        for(auto& dir:dirs){
            int x = t[1] + dir[0];
            int y = t[2] + dir[1];
            
            if(x<0 || y <0 || x>= m || y>= n || visited[x][y])
                continue;
            // push in queue the minimum neighbour of all neighbors.
            pq.push({min(t[0],A[x][y]),x, y});
        }
    }
    // NF
    return -1;
}

Find the city with smallest number of neighbors at a Threshold distance

Problem requires to run the shortest path Dijkstra at each node to get number of cities reachable from each vertex and then finding minimum of these cities.

This is classic SPSP : Single Pair shortest path problem!

Let’s talk about APSP : All pair shortest paths!

basically we are interested in the matrix $A_{ij}$ which find shortest path from $i$ to $j$

Two popular Algorithms that are quite useful for this task.

Floyd Warshall
Bellman Ford

Floyd Warshall

Lets say we have nodes 0, 1, 2, … , n-1

We have

$A_{ijk}$ : Shortest path from $i$ to $j$ that contains only vertices from $[V_0, … V_k]$ and not any other vertex.

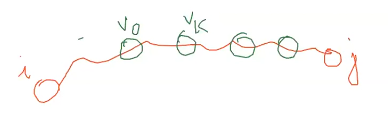
This problem can be solved using dynamic programming.

We can think of the $A_{ijk}$ as there are two possibilities : either the path contains the $V_k$ or it doesn’t pass thru $V_k$ and we want minimum of that.

$A_{ijk} = min(A_{ij (k-1)} , A_{ik(k-1)} + A_{kj(k-1)})$

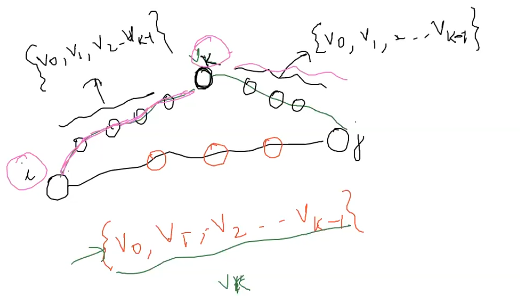
Note : on path $V_k$ can’t come again otherwise it will contain cycles!

Let’s talk about our old framework!

Order of iteration : 3D DP hmm…

k must be outer loop : this guarantees that we don’t end up requiring a value that has not been yet computed.

Base Case : $A(i,i) = 0$

There is only two possible : there is direct edge then that’s the answer or there is no edge then infinite.

Space state optimization :

can we do using 2D matrix ?

One solution to maintain 2, 2D matrices for current and previous k solution.
Its possible! find out. Trick is recursion! , does it matter if we update!

$A_{ikk}$ is same as $A_{ik(k-1)}$

int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
    vector<vector<pair<int,int>>> graph(n);
    vector<vector<int>> dp(n, vector<int>(n,INT_MAX));
    int i, j, k, count, res = INT_MAX, res_vertex;

    // Graph Construction and DP intialization.     
    for(const auto& edge : edges){
        graph[edge[0]].push_back({edge[1],edge[2]});
        graph[edge[1]].push_back({edge[0],edge[2]});
        // Base Case.
        dp[edge[0]][edge[1]] = edge[2];
        dp[edge[1]][edge[0]] = edge[2];
    }

    // Base Case.
    for(i = 0; i < n; i++)
        dp[i][i] = 0;
    
    for(k = 0; k < n; k++){
        for(i = 0; i < n; i++){
            for(j = 0; j < n; j++){
                if(dp[i][k] != INT_MAX && dp[k][j] != INT_MAX)
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
            }
        }
    }
    // Finding the solution.
    for(i = 0; i < n; i++){
        count = 0;
        for(j = 0; j < n; j++){
            if(dp[i][j] <= distanceThreshold)
                count++;
        }
        if(res >= count){
            res = count;
            res_vertex = i;
        }
    }
    return res_vertex;
}

Review :

SPSP : Single path shortest path

unweighted => BFS
weighted => PQ | Dijkstra’s Algorithm

APSP : All pair shortest path

Floyd Warshall (Dynamic Programming Solution)
- Space Optimization
- Recurrence
- Base Cases
- Fails when there are negative weights!
Tarzan’s Algorithm -

Tarzan’s Algorithm

Critical Connections in a Network

Any edge that is not part of cycle we can predict that is critical connection!

We will keep storing nodes we see into a vector and when we see a visited node that mean the recent edge actually led us to a cycle! and all those elements are part of the cycle.

We can give vertices ranks for the order we visited so we maintain ranks rather than visited array!

Node has 3 state

current path (current rank)
not in current path (n+1)
not in current path and not yet visited (-1)

We can make a rank vector {-1} initialized

int dfs(vector<vector<int>>& graph, int i, vector<int>& rank,
        vector<vector<int>>& res, int prev_rank, int n){
    rank[i] = prev_rank+1;
    int t = INT_MAX;

    for(const auto& nbr: graph[i]){
        if(rank[nbr] == -1){
            int k = dfs(graph, nbr, rank, res, prev_rank+1, n);
            if( k > rank[i] )
                res.push_back({i, nbr});
            t = min(t, k);
        }
        else if(rank[nbr] == n+1)
            continue;
        else if(rank[nbr] != prev_rank)
            t = min(t, rank[nbr]);
    }

    rank[i] = n+1;
    return t;
}
vector<vector<int>> criticalConnections(
    int n, vector<vector<int>>& connections) {
    // Construct the graph.
    vector<vector<int>> graph(n);

    for(const auto& edge : connections){
        graph[edge[0]].push_back(edge[1]);
        graph[edge[1]].push_back(edge[0]);
    }

    // Tarzan's Algorithm

    vector<vector<int>> res;
    vector<int> rank(n,-1);

    int k = dfs(graph, 0, rank, res, 0, n);

    return res;
}