Binary Search Tree
Ordered Search Structures (BST)
Whenever we are required to handle subarrays, we can think of it this way
A[i...j] = A[0..j] \ A[0..i-1]
( practice last question of Hashing)
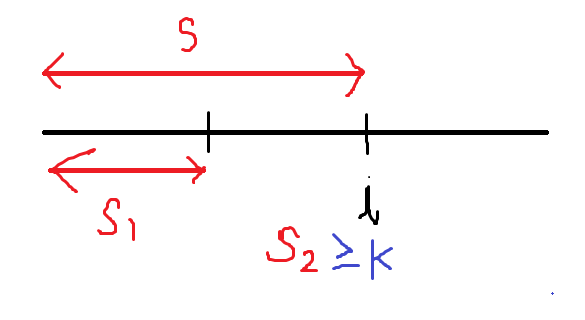
This is similar to previous question
So we want window with sum $s_2$ such that $ s_2 \ge k $ Here k is target.
No we can transform question into find the subarray with sum $ s_1 $ such that $s_1 \le k $ and as per question constraint we have to find such that it makes window of smallest size ( or most recent $s_1 $ that follows the criteria).
Now here thing to notice is that $s$ and $s_1$ can be precomputed considering its a prefix sum. So problem reduces to finding the largest prefix sum with $sum \le s-k$ for each $i$
Since numbers are positive so prefix sum will keep on increasing and we can do a binary search… $O(n\log n)$
Predicate : $s_1\le S-k$ Pattern : TTTTFFFFF, To find last T
or Predicate : $s > k$ Pattern : FFFFFTTTTT to find last F
int getLargestLessEquals(vector<int> &arr , int target){
int n = arr.size(), lo, mid, hi;
lo = 0, hi = n-1;
// F*t*
// p(x): arr(x) > target
// last F
while(lo < hi){
mid = lo + (hi-lo+1)/2;
if(arr[mid] > target)
hi = mid-1;
else
lo = mid;
}
if(arr[lo] <= target)
return lo;
return -1;
}
int minSubArrayLen(int target, vector<int>& nums) {
vector<int> prefix_sum;
prefix_sum.push_back(0);
int cum_sum = 0, window_length,res = INT_MAX;
// very important people forget it.. always
// add the sum that starts with 0
for(int i = 0; i < nums.size(); i++){
// ending at i; let's find out largest prefix sum <= cum_sum-target
cum_sum += nums[i];
prefix_sum.push_back(cum_sum);
// binary search ...
int idx = getLargestLessEquals(prefix_sum,cum_sum-target);
// everything is greater than cum_sum - target
if(idx == -1)
continue;
else{
window_length = i-idx+1;
res = min(res,window_length);
}
}
return res==INT_MAX? 0 : res;
}
Some information(prefix sum) is given ( history) and we need to search for item(largest value) with specific criteria(s > target) .
since here information (prefix sum) was in increasing order and we got away with searching using binary search in $O(\log n)$.
Not necessary that information is not sorted fashion.. still we require to look it up in $O(\log n)$ that is why we need Dynamic Ordered Search Structure.
We wanted largest sum so there must be ordering to find it.
BST , Heaps comes to save the day :)
BST promises
- Insert $O(\log n)$
- Delete $O(\log n)$
- Search for a key $O(\log n)$
Wait .. Hold up isn’t that all done by Hash Maps already and better? Moment :) BST is ordered. so we can get something more.
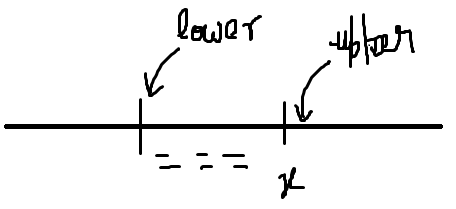
- Upper Bound (x) : smallest item > x
- Lower Bound (x) : smallest item >= x
| ———– ============= ————|
| x|
^(lower) ^(upper)
BSTs in C++ STL
remove unordered prefix from Hash Maps :)
map<int,int> m; its a BST !
int minSubArrayLen(int target, vector<int>& nums) {
int n = nums.size();
// key - prefix sum (search query on it)
// value - index
map<int, int> m;
//empty prefix
m[0] = -1;
int cum_sum = 0, window_length,res = INT_MAX;
for(int i = 0; i < nums.size(); i++){
cum_sum += nums[i];
// largest histor with prefix sum <= cum_sum - target;
// UB
auto it = m.upper_bound(cum_sum-target);
// UB-1
if(it == m.begin()){
m[cum_sum] = i;
continue;
}
else{
--it;
window_length = i-it->second;
res = min(res,window_length);
}
m[cum_sum] = i;
}
return res==INT_MAX? 0 : res;
}
Lets keep input sorted by starting time.
Lets assume we have intervals $I_1 , I_2 , I_3 , I_4, I_5, … .I_n$
all are disjoint and we want to add new interval $I_j (s_i, e_j)$
Assume $I_j$ can be inserted in $I_4$ and $I_5$ without loss of generality
There are 4 cases possible.
$I_j$ intersects with $I_4$
$I_j$ intersect with $I_5$
$I_j$ intersects with both
$I_j$ intersects with none
All cases can be defined in terms of start values and end values too.
overlap conditions $e_j > s_5$ or $s_j < e_4$
key concept here is understanding how lower bound works here.
// key - start time
// value - end time
map<int , int > m;
MyCalendar() {}
bool book(int start, int end) {
auto it = m.lower_bound(start);
// check if this interval overlaps with the lower bound
// this interval will end after the lower bound starts
if(it != m.end() && end > it->first ) return false;
// get the previous of lower bound
// check if this interval overlaps with the previous one
if(it != m.begin() && start < (--it)->second) return false;
// valid interval
m[start] = end;
return true;
}
Simplest solution take map < int , int > // key - start,end and //value - count
|————|
|————-| |—————–|
|—————-|
1 -1 1 1 -1 -1 1 -1
mark start as 1 then -1 as end.. Now just keep summing over and if u encounter sum as 3 that means more than 1 overlaps occurred.
Why here we use map : because we want to iterate increasing order of time..
so its accessing in sorted fashion of key thats what we want
map<int,int > m;
MyCalendarTwo() {}
bool book(int start, int end) {
// insert this interval
m[start]++;
m[end]--;
//check if overlap become 3 anywhere
int cum_sum = 0;
for(auto it : m){
cum_sum += it.second;
if(cum_sum == 3) {
// remove this interval
m[start]--;
m[end]++;
return false;
}
}
return true;
}
Hash Table guarantee insert delete O(1) But how to get Random element in O(1).
Simplest way is to use array but again it makes delete expensive.
hmm maybe we can use array and hashes together
good way is to insert in both HT and Array. Array solves randomness. but how to delete in array. ( search the element and swap with last ).
store values in unordered map <int ,int > here key - element inserted, and value - as index.
Now insert is in both O(1).
for delete we need to first search in hash table we can find index in O(1) and then delete using swap with last element. // we solved array deletion problem.
for random just do random index picking on vector
unordered_map<int, int> m;
vector<int> v;
RandomizedSet() {}
bool insert(int val) {
if(m.find(val)!= m.end()) return false;
// insert in vector
v.push_back(val);
// insert in map
m[val] = v.size()-1;
return true; }
bool remove(int val) {
if(m.find(val) == m.end()) return false;
// remove from vector
swap(v[m[val]] ,v[v.size()-1]);
v.pop_back();
//change the index of new element inserted
m[v[m[val]]] = m[val] ;
// remove from map
m.erase(val);
return true; }
int getRandom() {
int random_indx = rand()%(v.size());
return v[random_indx]; }