> Problems : Basics 2 > Linked Lists

Linked Lists

Non-Linear DS

None of the DS we practices was quick at searching. We want a DS with the following capabilities

Insert
Delete
Find/Search

DAT

We can use array for marking the existence of a element.

Drawback

Wastage of Space (Sparse Array)
Input Range should be known ahead of time
Input has to be integers
Input range is small

Improvement

Lets fix small range and use a mapping function $f$ whose output is fixed in the range specified. So hashing fixed above drawbacks to a degree.

But introduces some more complexity or bottlenecks

$f$ computation should be fast and one-one
$f$ should be deterministic ( always consistent and same output)

$f$ should be one-one but is it possible always ? NO!

because domain > range : this is so because range (aka DAT) is finite and expected to be small in size.

So there is a need to handle hashing collision

How to design such $f$ . We consider input to be gaussian/normal then $f$ we want to produce uniform output

Collision Handling

Chaining
Open Addressing (linear probing)

Applications

Frequency application
Subarrays
Other Problems like grouping (like frequency counting)
Store history and look up at it (fraction , prison cell, subarray with sum k)

Hashing in STL

Sets

Unordered Set

Allow only unique items once

unordered_set<int> s;
s.insert(32);
s.erase(32);
s.find(32); // returns iterator for hit to the item for miss to the end of set

Unordered Multiset

Allow multiple copies

Unordered Map

<k,v> : key, value pair

unordered_map<string,userObj> m;
m.insert({"smk",obj});
m["smk"] = obj;
m.erase("smk");
m.find("smk"); // returns iterator for hit to the item for miss to the end of map

Problems

Brick Walls Problem bounds doesn’t allow using the DAT

So we can use a map for counting frequency for counting the corners (brick edges) and find the max edge in such map.

why can’t we use DAT ? reason 1. can’t get array of INT_MAX size 2. line that cuts brick doesn’t pass thru edges every time xD so we don’t need to store those cases.

int leastBricks(vector<vector<int>>& wall) {

    unordered_map<int,int> m;
    int i,j, pos, max_count = 0;
    for(i = 0; i< wall.size(); i++){
        pos = 0;
        for(j = 0; j < wall[i].size()-1; j++){ // wall.size()-1 for leaving the last boundary
            //calculate the position
            pos += wall[i][j]; 
            m[pos]++;
            max_count = max(max_count,m[pos]);
        }
    }

    return wall.size()-max_count;
}

Rabbits in Forest

Way to approach this problem is making chunks of each color of rabbit, chunk size we can infer from the number of rabbits say a rabbit says there are 2 rabbits with the same color then there are 3 rabbits for sure that have same color.

Now what we can do is consider that other 2 rabbits asked same question and they answered same amount then these are the rabbit first one talked about ( why because we want min color).

So basically problem reduces to do the frequency table and then divide then frequency into chunks using $\lceil \frac{cnt}{num+1} \rceil = \frac{5}{2+1} = 2 $

but we need to multiply each chunk with the weights of the numbers to get correct rabbits number.

i.e rabbits are $numchunks = 22 = 4$ i.e. (blue and red rabbit)

so $ \text{ total rabbits }= \Sigma_{i=1}^{i = n} \ (i+1) \lceil \frac{c_i}{i+1} \rceil $ .

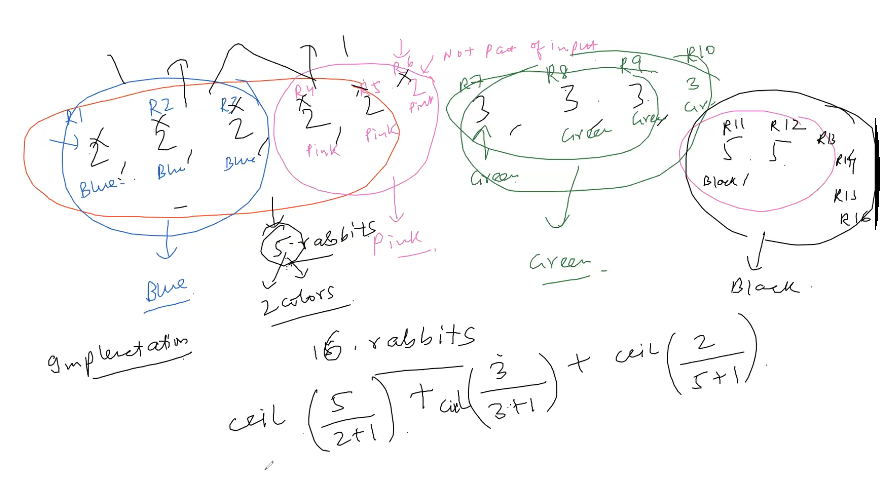
do remember : res += (i+1) * ceil((double)arr[i]/(i+1));

Here double is quite important because there is nothing to be ceil to act on because integer division already yields integer for you and to get a ceil value there must be decimal value :)

Group Anagram : Simple problem , but try to achieve simple implementation

use simple hash map with value vector<string> (list of anagrams) and key = (identifier for group) : here two possibility vector of 26 size or we can sort all strings.

which one is better ? sorting will be expensive for long strings so DAT of 26 is good enough key

unordered_map<vector<int>, vector<string>> m; // syntax error :)
 // we can't hash vectors not unless we define hash function
// or use a hash range
unordered_map<string, vector<string>> m;
unordered_map<int, vector<string>> m;
// both are not optimized for space

better approach is to store values of map as indices that indicate location on the result vector :) and another improvement is that create a unique string as key (kind of like vector<int>) see the getIDdfunction :)

Solution.

string getGroupId(string &s){
    vector<int> freq(26,0);
    for(auto &ch : s){
        freq[ch-'a']++;
    }

    string res = "";
    for(int i = 0;i < 26; i++)
        res+= to_string(freq[i]) + "#"; // "#"delimiter for our key:)

    return res;
}
vector<vector<string>> groupAnagrams(vector<string>& strs) {
    vector<vector<string>> res;
    unordered_map<string,int> m;
    int i;

    for(i = 0; i < strs.size(); i++){
        // get the group identifier
        string id = getGroupId(strs[i]);

        // if this is the first element of the group 
        if(m.find(id) == m.end()){
            m[id] = res.size(); //location to insert string in vector
            res.push_back({});
        }
        res[m[id]].push_back(strs[i]);
    }
    return res; 
}

Prison Cells After N Days One possible solution is taking xor’s of elements neighbor n times. not efficient quadratic time complexity.

hmm.. sounds difficult. read the problem again it says 8 prisons. does that ring a bell ?

we observe cycles! because only 256 combination , and there is definite way to change states. Hmm .. can we detect cycle or the size of cycle that we don’t need to rotate thru cycles :) just we can directly claim the answer..

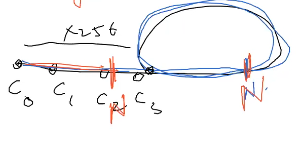
Strategy - > min ( N , #iteration to get a repeating state for the first time…) - > <= 256

we can store key as config :)

string getNextConfig(string &curr_config){
    string next_config(8,' ');
    next_config[0] = next_config[7] = '0';
    for(int i = 1 ; i < 7; i++)
        next_config[i] = curr_config[i-1] == curr_config[i+1] ? '1' : '0';
    return next_config;
}
vector<int> prisonAfterNDays(vector<int>& cells, int N) {
    // key - configuration
    // values - Iteration count when it occured for the first time
    unordered_map<string, int> m;
    vector<string> conf;
    string res;

    int i = 0,cycle_length;
    string init_config(8,' ');
    for(i = 0; i < 8; i++)
        init_config[i] = cells[i]+'0';

    string curr_config = init_config,next_config;
    m[init_config] = 0;
    conf.push_back(init_config);
    for(i = 1; i <= N; i++){
        next_config = getNextConfig(curr_config); 

        // Cycle
        if(m.find(next_config) != m.end())
            break;
        // not a cycle
        // insert in the map
        m[next_config] = i;
        // push in the vector
        conf.push_back(next_config);
        // update current config
        curr_config = next_config;
    }

    if( i == N+1 ) // found the config before the cycle :)
        res = next_config;
    else {
        // computation for cycle :)
        // tail lenth is where the cycle happens first time
        int cycle_length = i - m[next_config];
        int tail_length = m[next_config];

        int j = (N-tail_length) % cycle_length;

        res = conf[tail_length+j]; 
    }

    // return the vector of res :)
    vector<int> ans(8);
    for(int i = 0; i < 8; i++) ans[i] = res[i]-'0';
    return ans;
}

Fraction to Recurring Decimal : Difficult implementation problem and too many edge cases. Conceptually we keep multiplying numerator with 10 for each time we take quotient and remainder and use a map to check whether that numerator has appeared before or not. If it has appeared already that means its recurring fraction (cycle starting point). and rest is just implementation complexity :)

Solution : http://p.ip.fi/QszV

Subarray sum equals K : lets practice this well known question.

Here can we use 2 pointers ? :) nope negative numbers. Way 2 pointer work because of j monotonically increase or decrease with respect to i. if graph of j vs i is either increasing of decreasing. Here its not this because of negative numbers :)

Think about Prefix Sum. There are n types of subarrays which end at 0 , end at 1 , … , end at i, … end at n-1.

use a map : key -> prefix sum

value -> number of prefix with that prefix sum

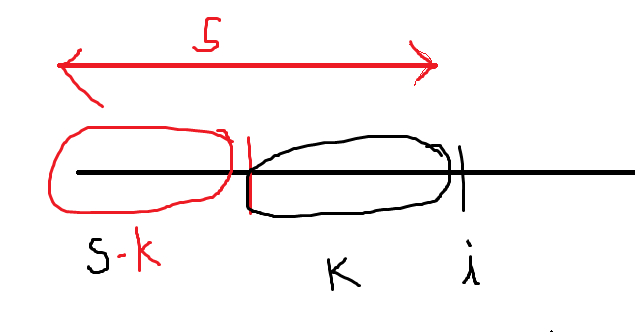
Above diagram shows that finding the window of sum K is equivalent to finding all the prefix sum arrays within the bound i, with sum s-k.

int subarraySum(vector<int>& nums, int k) {
    int n = nums.size(), i, cum_sum = 0, res = 0;
    unordered_map<int, int> m;

    // empty prefix array
    m[0] = 1;
    for(i = 0; i <n; i++){
        cum_sum += nums[i];

        res += m[cum_sum-k];
        m[cum_sum]++;
    }
    return res;
}