Linked Lists
Basic Problems
Reversing a Linked List
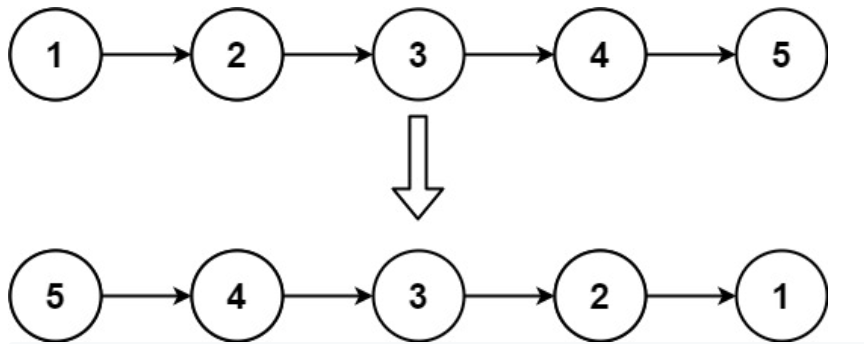
There can multiple ways to do this but simplest is just making a new head and keep pushing items on the new head ( reverse automatically)
link reverse(link head){
link x = head; // copy of head ( good practice )
link rev = nullptr,tmp ;
while(x){
tmp = x->next; // increment the list
x -> next = rev;
rev = x;
x = tmp;
}
return rev;
}
// its a suffix subproblem case
Recursive approach
// head is declared globaly
link rev(link x){
if(x == nullptr) return nullptr;
if(x->next == nullptr){
head = x;
return x;
}
link node1 = rev(x->next);
node1->next = x;
x->next = nullptr;
return x;
}
Important Algorithms
Floyd’s tortoise and hare
Given a linked list with cycles find whether the list contains cycle of not.
Solution : Its quite simple just consider two pointers but they move at different speed. Fast pointer goes into cycle before the slow one and if there exists a cycle they are guaranteed to meet somewhere in the cycle.
Code Illustration
// suppose a struct node exists. and link is just typedef on *node
link isCycle(link head){
link slow = head , fast = head;
while(!fast && !fast->next && slow!=fast){
slow = slow -> next;
fast = fast -> next -> next;
}
// the moment loop ends we hit the point at which both meet
if(!fast || !fast->next) return nullptr;
return slow;
}
// above function returns null if there is no cycle else it return the point where the cycle exists.
Property: Slow pointer always travels half of the fast pointer.
Problem Extension :
Find the moment where the cycle started. Refer to figure.
lets say $n$ represent the distance where the cycle started and $k$ where the turtle and hare meet after some revolutions. And lets assume cycle is of size $m$.
let, distance traveled by slow = $i$ , then distance by fast pointer = $2i$.
lets simulate the run. $i = n + m*p_1 + k $ where $ p_1 :$ number of cycle it took to hit the meeting point.
similarly for fast pointer $ 2i = n + m * p_2 + k $ here $p_2 :$ number of cycle for fast pointer.
Simplifying $n+k = m * (p_2 - 2p_1)$
or we can see it as $ n + k = m * integer$ .This implies $n+k$ always wraps around circle.
or Diamond point is n distance (direction of cycle) away from head of list.
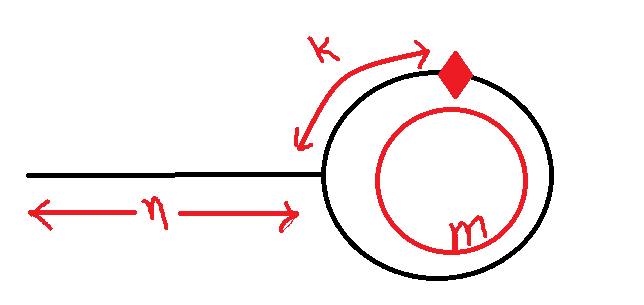
link diamond = isCycle(head), hptr = head; // good practice to not change given head
while(diamond!=hptr){
diamond = diamond->next;
head = head->next
}
This problem is excellent demonstration of above concept xD;
Possible ways are n number sum, xor ( failed cause repeating numbers can be more than 1 ).
we can maintain visited array. extra space O(n) ;)
we can fix space usage by using negative numbers as markers using this nums[abs(nums[i])] = -1 nums[abs(nums[i])] .
also we can sort and find neighbors with same value.
best solution is using the above concept.
visualize : nums = [1, 3, 4, 2, 2]
think empty link linked (val -> null) while there is a next link which is defined by the num[i] ;) so nums[i] acts as link for linked list traversal right , so we can traverse array in specific manner ( similar to linked list)
slow = nums[i];
fast = nums[nums[i]];
:-)
Some problems and their hints :
Just find the mid point using slow and fast pointer and then reverse the second half of list and compare.
Use the slow and fast pointer approach but :D at n distance, just be careful of edge cases.
Insert at the head as well as tail. Connecting various groups.
Medium Questions
// lookup merge step of merge sort
void insert(link *r,link *h){
(*r)->next = (*h);
(*h) = (*h)->next;
}
link merge(link h1, link h2){
link res = new ListNode();
link ans = res;
while(h1!=NULL || h2!=NULL){
if(h1 == NULL) { insert(&res,&h2); break;}
if(h2 == NULL) { insert(&res,&h1); break;}
if(h1->val <= h2->val) insert(&res,&h1);
else insert(&res,&h2);
res = res->next;
}
return ans->next;
}
Use recursion.
// Recursion Revisited…
How can we get the function to return values. Two ways : either returning explicitly or using implicitly ( arguments passed by reference).
Explicitly returning function
int f(..) {
/// some body
}
when we call this function we can store it in a variable say int y= f(..) and then we can operate on y
another way
Implicitly returning function
we can declare y ahead of time and call the function with y as a argument (passed as reference) and then function actually changes the y.
Solution when lists are of equal length.
Now real catch is both are unequal size… :D
What if we pad the unequal linked list to get them to equal size :)
// code is still buggy (to do fix it)
link f(link l1, link l2, int &carry){
if(!l1){
carry = 0;
return nullptr;
}
int passed_carry;
link summed_list = f(l1->next,l2->next,passed_carry);
int curr_elt = (l1->val + l2->val + passed_carry)%10;
int curr_carry = (l1->val + l2->val + passed_carry)/10;
link curr_node = new ListNode(curr_elt);
curr_node -> next = summed_list;
// implicit return
carry = curr_carry;
// explicit return
return curr_node;
}
link addTwoNumbers(link l1,link l2){
//------------------------------------------------------
// Padding Logic
link curr_l1 = l1, curr_l2 = l2;
while(curr_l1 && curr_l2){
curr_l1 = curr_l1->next;
curr_l2 = curr_l2->next;
}
ListNode dummy;
link new_l1,new_l2,pad_list = &dummy,rem_list;
if(curr_l1){
rem_list = curr_l1;
new_l1 = l1;
pad_list->next = l2;
} else {
rem_list = curr_l2;
new_l1 = l2;
pad_list->next = l1;
}
// creating padding zeros.
while(rem_list){
link tmp = new ListNode(0);
tmp->next = pad_list->next;
pad_list->next = tmp;
rem_list = rem_list->next;
}
// pad_list has all 0s we need;
new_l2 = pad_list -> next;
// new_l2 is always shorter list
// l1 is always longer list
//------------------------------------------------------
int carry;
link res = f(new_l1,new_l2,carry);
link curr = res;
if(carry){
curr = new ListNode(carry);
curr-> next = res;
}
return curr;
}