Stacks
Review :
Dynamic Data Structure , O(1) insert, remove latest insertion and lookup top.
Application for practice.
- Expression Evaluation
- Monotonic Stack
- Generic Problems
USP (Unique Selling Point xD) of stack.
- LIFO property
Problems on Implementations and Designs
Min Stack : Implementation problem. Use 2 stack. One for keeping track of stack ops and one stack for maintaining minimum so far.
Custom Stack : Use a vector to implement stack and desired function. (gives AC) (naïve approach not desired).
Interesting Implementation :
lazy increment take O(k) to implement but remember function doesn’t return anything and doing this operation can be costly if done frequently.
Don’t increment at the time increment is called rather while popping ensure its popped with correct value.
Keep the stack with pair <int , int > now while incrementing just to the change at the kth element. and while popping keep transferring the previous increments all the way to the bottom of stack.
this reduces the cost to O(1)
class CustomStack {
public:
vector<int> custom_stack_; // keeps track of stack
vector<int> inc_val_; // keeps track of increment value
int size_;
CustomStack(int maxSize) {
size_ = maxSize;
}
void push(int x) {
if(custom_stack_.size() == size_)
return;
custom_stack_.push_back(x);
inc_val_.push_back(0);
}
int pop() {
if(custom_stack_.empty())
return -1;
int last = custom_stack_.back() + inc_val_.back();
// transfer before removing
if(custom_stack_.size() > 1){
inc_val_[inc_val_.size()-2] += inc_val_.back();
}
custom_stack_.pop_back();
inc_val_.pop_back();
return last;
}
void increment(int k, int val) {
int n = custom_stack_.size();
if(n == 0) return; // edge case
inc_val_[min(n,k)-1] += val; // adding on increments.
}
};
Maximum Frequency : A useful and more precise approach would be to maintain a map of frequency which is of type stack.
so for freq 1 we have a stack
for freq 2 we have a stack
if we want to insert say push(5) we insert in freq1 stack once and push once in freq2 stack
push(5), push(7) ,push(5)
1 – | | => stack => 5,7
2 – | | => stack => 5
Now its quite easy to infer 5 is most frequent and we have to pop it.
It solves two problems : popping the max frequency as well in the case of tie we pop most recent insertion.
We will need another integer DAT for storing frequency.
class FreqStack{
public:
int max_freq;
unordered_map<int,int> counter; // DAT
unordered_map<int,stack<int>> rev_freq;// the table shown in digram
FreqStack(){
}
void push(int x){
//increase the counter
counter[x]++;
int count = counter[x];
rev_freq[count].push(x);
// update the max_freq
max_freq = max(max_freq,count);
}
int pop(){
//remove the most frequent
int last = rev_freq[max_freq].top();
rev_freq[max_freq].pop();
//update the count
counter[last]--;
//update the max_freq
if(rev_freq[max_freq].empty()){
max_freq--;
}
return last;
}
};
Problems on Expression Evaluation
_fix is defined on operator
a b + Postfix
a + b Infix
+ a b Prefix
Reverse Polish Notation : Simple standard question.
Basic Calculator : Very famous question.
we can convert given expression to some standard notation (Postfix) then its quite easy to evaluate.
2nd way Processing Brackets smartly is the starting direction.
Now this expression has only +/- so we can think of - as negative numbers and we can easily push it to stack with sign xD. ( simplest way ) : keep pushing numbers and opening parenthesis until u hit closing parenthesis, now u can keep popping and until u find corresponding opening parenthesis. Now here we just need to add because we reduced the - as sum of negative numbers .
Parsing the spaces is also an issue.
StockSpanner : Very Good Problem on Monotonous Stack
Monotonous Stack have a property that at every point of time entries in stack are monotonic.
stack<pair<int,int>> mono;
int pos = 0;
int next(int price){
pos++;
while(!mono.empty() && mono.top().second <= price){
mono.pop();
}
int res;
if(mono.empty())
res = pos;
else
res = pos-mono.top().first;
mono.push({pos,price});
return res;
}
Above programs puts item in stack then digs (pop) the stack until it finds the price that is larger than current item’s price. And the result each time is just how far that item is from nearest largest price
calculated using the item number.
Based on Above problem there is a problem that says find the nearest max number ahead of the current element
Final Prices with a special discount in a shop : similar concept Monotonic Stack.
arr => 5 18 4 55 29 40
res => 18 55 55 -1 40 -1
we can use same concept as above but start processing in the opposite direction
see comments by lee215 and try more questions on the topic
Largest Rectangle in Histogram : for the largest rectangle there must be one such bar which is completely inside the rectangle.
Then for each bar we can calculate the maximum rectangle that it encapsulates and max of those numbers is the answer we are looking for :)
So lets understand how we will get the maximum rectangle which contains the bar. For each $h_i$ bar we will look for nearest smallest number on left and similarly we do for the right side.
summing that distance gives us widths.
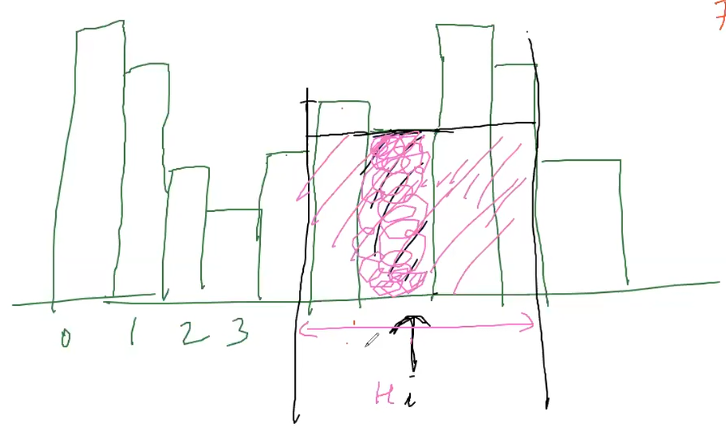
Area = $h_i * w $
Now we want to find nearest smallest on right and left. Use 2 monotonic stacks. Trivial
2 pass and O(n);
int largestRectangleArea(vector<int>& heights) {
int n = heights.size(),width,area;
int res = INT_MIN;
vector<int> rt(n);
stack<int> r;
for(int i = n-1; i >= 0 ; i--){
while(!r.empty() && heights[r.top()] >= heights[i])
r.pop();
if(r.empty())
rt[i] = n;
else
rt[i] = r.top();
r.push(i);
}
stack<int> s; // assume as index
// populate both vector with nearest number which is less
for(int i = 0; i<n ; i++){
while(!s.empty() && heights[s.top()] >= heights[i])
s.pop();
if(s.empty()){
width = rt[i];
}
else{
// width = left smallest + right smallest - 1
// width = (i- s.top())+ (rt[i]-i-1)
width = rt[i]-s.top()-1;
}
area = heights[i]*width;
res = max(res,area);
s.push(i);
}
return res;
}
Challenge use single pass and no array and precomputation.
Only stacks xD
hmm area does seem monotonic for each bar , if we think of right boundary as the height in focus then we just need left closest smallest boundary then its just the case of monotonic stack and maintaining area.
int largestRectangleArea(vector<int>& heights){
// extra padding for the case when there is no boundary
heights.push_back(0);
stack<int> st;
int n = heights.size(), i, res = INT_MIN,tp,right,left,area,width;
for(i = 0; i<n ; i++){
while(!st.empty() && heights[st.top()] >= heights[i]){
tp = st.top();
st.pop();
right = i;
left = st.empty()?-1:st.top();
width = right - left - 1;
area = width * heights[tp];
res = max(res,area);
}
st.push(i);
}
//remaining elements without a right boundary
return res;
}
Maximal Rectangle : Find the maximum rectangle that is 1 in a 2D Matrix.
Just apply on each column for each row this operation and take height as continuous sum;
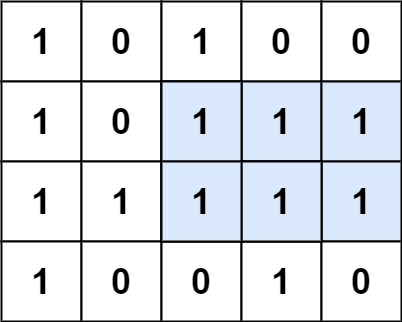
1 0 1 0 0
2 0 2 1 1
3 1 3 2 2
4 0 0 3 0 This is how dp matrix looks like. and apply above histogram function on each row :).
int maximalRectangle(vector<vector<char>>& matrix) {
if(matrix.size() == 0) return 0;
int m = matrix.size() , n = matrix[0].size();
int res = INT_MIN;
vector< vector<int>> dp(m, vector<int>(n));
// processing the dp
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++)
if(matrix[i][j] == '1' && i > 0)
dp[i][j] = dp[i-1][j] + (matrix[i][j]-'0');
else{
dp[i][j] = (matrix[i][j]-'0');
}
}
for(auto x: dp){
int lRectangle = largestRectangleArea(x);
res = max(res,lRectangle);
}
return res;
}