Trees-2
Solving Question on Trees
- Think about solving the same problem or a modified version for the left and right subtrees
- Combine these solution to solve the original problem
- Needed to return more than 1 values
LCS ( Lowest Common Ancestor )
It has many practical and direct applications and its one of the most important algorithm to learn.
Top Down
LCS node is the node that is the first node where p , q are on different subtree.
LCA will store the lowest common ancestor in “res” & will return true if either p or q exists in the subtree rooted at “root”.
Best do a try run of this code. important points to notice how we deal the node itself being the ancestor.
typedef TreeNode* link;
bool lca(link root, link p, link q, link *res){
if(!root)
return false;
bool l1 = lca(root->left,p,q,res);
bool l2 = lca(root->right,p,q,res);
if( (l1 && l2) || ((root == p || root == q) && (l1 || l2)))
(*res) = root;
return (l1 || l2 || root == p || root == q);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
link res = NULL;
bool l = lca(root,p,q,&res);
return res;
}
Tree Traversal
Post-Order : left -> right -> root (this takes decision based on results from subtrees)
Pre-Order : root-> left -> right (passing down the contribution)
In - Order : left -> root-> right
Level-Order : travel nodes in a level
Post-Order utilizes the solutions from subtrees to get the solution.. (very useful)
Level Order Traversal
very standard problem use a queue to maintain order
this is a BFS based solution
typedef TreeNode* link;
vector<vector<int>> levelOrder(TreeNode* root) {
queue<link> q;
vector<vector<int>> res;
if(!root) return res;
q.push(root);
while(!q.empty()){
int n = q.size();
res.push_back(vector<int>());
for(int i = 0;i < n ; i++){
link t = q.front();
q.pop();
res[res.size()-1].push_back(t->val);
if(t->left)
q.push(t->left);
if(t->right)
q.push(t->right);
}
}
return res; }
DFS ( preorder traversal)
void dfs(TreeNode *root, int depth,vector<vector<int>>& ret)
{
if(root == NULL) return;
if(ret.size() == depth)
ret.push_back(vector<int>());
ret[depth].push_back(root->val);
dfs(root->left, depth + 1);
dfs(root->right, depth + 1);
}
vector<vector<int> > levelOrder(TreeNode *root) {
vector<vector<int>> res;
dfs(root, 0,res);
return res;
}
There are tradeoffs, for very ’lean’ tree (most non-leaf node have only one child), this dfs approach consume O(n) memory, while BFS approach with queue cost almost constant space. For near complete tree (most non-leaf node have two child), DFS approach cost O(log(n)) memory, whereas BFS approach cost O(n) memory.
Binary Tree Level Order Traversal II : try to do in single loop rather than reversing.
lets do it using postorder.
What we need information from subtrees to populate final answer , we need height that will help us simplify index for result vector.
f populates the level order traversal Qn in the vector, o and it also return the height of subtree rooted r
just or do dfs change the last return line return res; to return vector<vector<int>> (res.rbegin(),res.rend());
void right(TreeNode* root, int ht, vector<int>& res){
if(!root)
return;
int n = res.size();
if( n-1 < ht){
res.push_back(root->val);
}
right(root->right, ht+1,res);
right(root->left,ht+1,res);
}
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
right(root,0,res);
return res;
}
More Problems
Populating Next Right Pointers in Each Node Doing the question using queue is quite easy.
Try to do it constant space
link connect(link root){
if(!root) return root;
root->next = NULL;
link curr_lvl = root;
link first_node_next_level;
first_node_next_level = NULL;
link curr_node = curr_level;
while(curr_lvl){
while(curr_node){
if(curr_node->left){
curr_node->left->next = curr_node->right;
if(curr_node->next);
curr_node->right->next = curr_node->next->left;
else
curr_node->right->next = NULL;
}
curr_node = curr_node->next;
}
curr_node = curr_level->left;
curr_level = curr_node;
}
return root;
}
Similar question but not binary tree
typedef Node* link;
Node* connect(Node* root) {
if(!root) return root;
root->next = NULL;
link curr_level = root;
link curr_node = root;
link prev_node = NULL;
link first_node_next_level = NULL;
while(curr_level){
while(curr_node){
if(curr_node->left){
if(prev_node)
prev_node->next = curr_node->left;
prev_node = curr_node->left;
if(!first_node_next_level)
first_node_next_level = curr_node->left;
}
if(curr_node->right){
if(prev_node)
prev_node->next = curr_node -> right;
prev_node = curr_node->right;
if(!first_node_next_level)
first_node_next_level = curr_node->right;
}
curr_node = curr_node->next;
}
curr_level = curr_node = first_node_next_level;
first_node_next_level = NULL;
prev_node = NULL;
}
return root; }
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
We don’t need to track all NULLs.
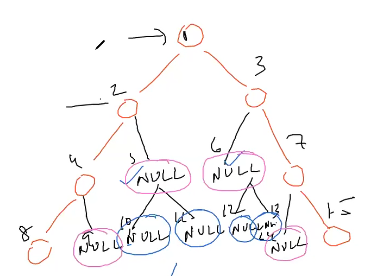
lets do a preorder traversal will give a good serialized string
1, 2, 4, 8, NULL, NULL, 3, NULL, 7, NULL, 15
how to deserialize , pass indices as index.
This implementation barely passes bounds but it works
typedef TreeNode* link;
void pre_serialize(link root, string& s){
if(!root){
s += ",n";
return;
}
s = s + "," + to_string(root->val);
pre_serialize(root->left,s);
pre_serialize(root->right,s);
}
link pre_deserialize(stringstream& ss){
string val;
getline(ss,val,',');
if(val == "n")
return NULL;
link node = new TreeNode(stoi(val));
node->left = pre_deserialize(ss);
node->right = pre_deserialize(ss);
return node;
}
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string serial = "";
pre_serialize(root,serial);
return serial.substr(1,(int) serial.size()-1);
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
stringstream ss(data);
return pre_deserialize(ss);
}
do the problem of serialize and deserialize BST. just do a preorder traversal no need of maintaining nulls.
Why we serialize the data
- Transfer over the network
- Persist on disk ( file / DB )
JSON is cheap way to serialize :) but its not safe and not compact.