Predicate Framework of Binary Search
Binary Search
- Predicate Framework
Key elements related to search.
- Search Space
- Item : certain properties
- Algorithm
Binary Search is a search algorithm which utilizes some property of search space.
- When can binary search be applied ?
- What all can be find ?
- Pseudo Code.
Terminology
-
Predicate : Boolean functions.
Boolean function maps items to $f : D\rightarrow {T,F}$, true or false.
-
Apply Predicate on a Search Space
Defining the predicate value of each item.
-
When is BS applicable
Binary Search is applicable $iff$ $\exists$ a predicate s.t. when you apply the Predicate on the search space s.t. the relation $p(x) \implies p(y)\ \forall y > x$ is true when we apply the predicate on search space.
If $p(x)$ is True then $p(y)$ is True $\forall y > x$
Means its a series like this : FFFFFFTTTTTTTTT (F*T*)
So if this statement is true then its contrapositive is also true.
$\neg p(y) \implies p(x)\ \forall y > x$
Means its a series like this : TTTTTTTTTFFFFFF (T*F*)
-
If Binary Search is applicable then what can u conclude
- In (F*T*) we can find last F and first T.
- In (T*F*) we can find last T and first F.
Strategy to solve Binary Search Problems
- Find ordering and a predicate s.t. F * T* and finding the last F or the first T will solve the problem.
Question
Find the first and last position of an element (target) in the array.
e. g. $A= [2,2,5,5,7,7,7,9,10,15]$ , target = 7.
Answer will be : [4,6] (assuming 0 indexing).
First Position : p(x) : ?? Find predicate ??
Predicate should reduce it to (F*T *) and last F / last T should give answer.
Simple p(x) : x >= target and first T solves the problem or alternatively x < target and first F.
Similarly for last position : p(x) : x <= target and last T solves the problem.
-
Pseudo Code for F * T *
-
last F
lo = first_elt, hi = last_elt; while(lo < hi){ mid = lo+(hi-lo+1)/2 if(p(mid)) hi = mid-1; else lo = mid; } // one element if(!p(lo)) return lo; return -1; -
first T
lo = first_elt, hi = last_elt; while(lo < hi){ mid = lo + (hi-lo)/2; if(p(mid)) hi = mid; else lo = mid+1; } // one element if(p(lo)) return lo; return -1;
There are 2 mid
- odd elements : well defined mid = (lo+hi)/2 = lo + (hi-lo)/2 (overflow fix)
- even elements
- low_mid = (lo+hi)/2 = lo + (hi-lo)/2 (overflow fix)
- high_mid = lo + (hi-lo+1)/2
- so we will decide mid is look inside if construct of predicate
- includes mid element = low_mid
- doesn’t mid element = high_mid
-
-
Pseudo Code for T*F*
- Last T
- First F
Find minimum in Rotated sorted array
Predicate Framework! We want to reduce it to F* T* format and find the last F/first T.
If we plot the values on a graph we see that values in any rotated array will be like this
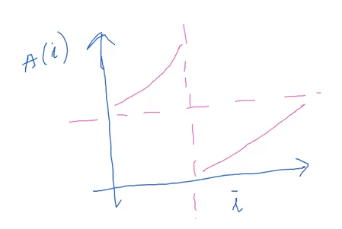
We see that the threshold is at first element. We want predicate such that above threshold it gives us false and True for other values.
$p(x) : x < A[0]$
and we want first T
int findMin(vector<int>& nums) {
if(nums.empty()) return 0;
int n = nums.size();
int lo = 0,hi = n-1;
while(lo < hi) {
int mid = lo + (hi-lo)/2;
if(nums[mid]<nums[0]) hi = mid;
else lo = mid+1;
}
if(nums[lo] < nums[0]) return nums[lo];
else return nums[0];
}
Peak index in a mountain array
predicate : slope :=A[i] > A[i+1] type F* T* solution first T
int peakIndexInMountainArray(vector<int>& arr) {
int n = arr.size(),lo,hi,mid;
int lo=0,hi=n-1;
while(lo < hi) {
mid = lo + (hi-lo)/2;
if(arr[mid] > arr[mid+1])
hi = mid;
else
lo = mid+1;
}
// no need of sanity check (given in question!)
return lo;
}
Optimization Problems
Problems where we have to optimize a variable under some constraints.
- What kind of optimization problems can Binary Search enable to solve ?
- Systematic approach for identifying such problems & solving them.
Find the Smallest divisor given a threshold
So this problem represents a group of classic problems which are basically based on guessing the solution! How can we guess the solution ? Notice every solution to problem (consider solves or not) exhibits monotonicity !
If one solution solves the problem then all the previous solution will solve the solution.
So basically keep guessing divisor if solution doesn’t match decrease upper bound and if this is a solution then increase lower bound until we found a point where monotonicity changes ( first F , last T).
Lets say inflexion point is $x_k$
for all $x_i < x_k$ , $s_i > t$
$x_i \ge x_k$ , $s_i \le t$
Then problem is F* T*
int getSum(vector<int>& nums, int k){
int sum = 0;
for(int i = 0; i < nums.size(); i++)
sum += ceil((float)nums[i]/k);
return sum;
}
int smallestDivisor(vector<int>& nums, int threshold) {
int max_elt = INT_MIN, i, n = nums.size(), lo, hi, mid;
for(i = 0; i < n; i++)
max_elt = max(max_elt,nums[i]);
lo = 1, hi = max_elt;
while(lo < hi){
mid = lo+(hi-lo)/2;
if(getSum(nums,mid) <= threshold)
hi = mid;
else
lo = mid+1;
}
return lo;
}
Above problem was solvable because x under certain condition was monotonic.
Approach
-
Define Search Space -> x
-
Trim SS (from both ends)
-
p(x) <- constraint
f(x) <= t or f(x) >= t
-
first T