Binary Search continued ....

Two kinds of problems we can solve using Binary Search

  • Explicit Search Problems
  • Optimization Problems (monotonic)

Capacity to Ship Packages within D days

Cues : Optmization Problem.

  • min/max { x } st $f(x) \le threshold$ or $ f(x) \ge threshold$
  • $f(x)$ should be monotonic wrt x

here $x: capacity$ while $RT : f(x)$ , RT : # round trips

Triming Search space :

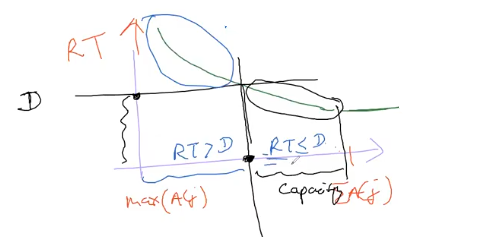
left = $max {A[j]}$ because capacity should be greater than max elt to load it on cart!

right = $ \Sigma A[j]$ we can send all of them in 1 go

  1. Search Space = [ $ max(A[j]), \Sigma A[j]$]

  2. Predicate

    image-20210512111701958

    This is F* T* with first T being answer to solution.

int getRoundTripTime(int C, vector<int>& weights){
    int i, curr_load = 0, rt = 0;
    for(i = 0; i < weights.size(); i++){
        if(curr_load + weights[i] <= C)
            curr_load += weights[i];
        else{
            rt++;
            curr_load = weights[i];
        }
    }
    // Count the last trip
    rt++;
    return rt;
}
int shipWithinDays(vector<int>& weights, int D){
    int n = weights.size(), i, lo, hi, mid, max_wt=INT_MIN, sum_wt = 0;

    for(i = 0; i < n; i++){
        max_wt = max(max_wt,weights[i]);
        sum_wt += weights[i];
    }

    lo = max_wt, hi = sum_wt;
    while(lo < hi){
        mid = lo + (hi-lo)/2;
        if(getRoundTripTime(mid,weights) <= D)
            hi = mid;
        else
            lo = mid+1;
    }
    return lo;
}

Find K closest Elements

Key point worth noticing here is that the distance of other values from pivot point is like a inverted pyramid. difference array should be monotonic.

Now can we predict dif(i+k) from dif(i)

So solution is $dif(i) \le dif(i+k)$

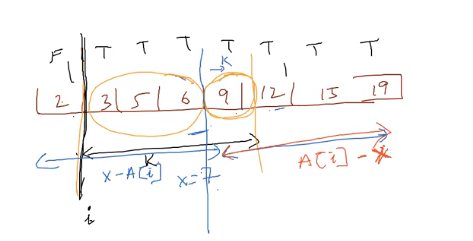
image-20210512113657291

we are interested in finding the value of $i$ using binary search.

Predicate : $p(i)$ : $x-A[i] \le A(i+k)-x$

vector<int> findClosestElements(vector<int>& arr, int k, int x){
    int n = arr.size(), lo, hi, mid;
    arr.push_back(10001);
    lo = 0, hi = n-k;
    while(lo<hi){
        mid = lo+(hi-lo)/2;
        if(x-arr[mid] <= arr[mid+k]-x)
            hi = mid;
        else lo = mid+1;
    }
    return vector<int>(arr.begin()+lo, arr.begin()+lo+k);
}

First Missing Positive

Upper bound of answer is n+1

First approach is to DAT (Direct Addressing Table) O(n) (time) with O(n) : space.

Second Approach

  • Go thru the array , change the -ve number to INT_MAX

  • go thru the array for i -> arr[i]

    $arr[arr[i] - 1] = -1*ar[ar[i]-1]$ if $arr[arr[i] - 1] > 0$

  • Go thru the array, return $i+1$ for the first $i$ such that $arr[i] $> 0

Ideas

  • DAT
  • Use the input array and the space
  • Preserving 2 things
    • Value
    • Vi

Search a 2D Matrix

Simple straight forward problem.

Search row and then search column. Complexity $O(\log m + \log n)$

or think of a single sorted array! :)

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    int n = matrix[0].size();
    int m = matrix.size();
    int i,j,mid;
    int lo = 0,hi = m*n-1;
    while(lo<hi){
        mid = lo+(hi-lo)/2;
        i = mid/n;
        j = mid%n;
        if(matrix[i][j] >= target) hi = mid;
        else lo = mid+1;
    }
    i = lo/n; j = lo%n;
    if(matrix[i][j] == target) return true;
    return false;
}

This is simple to see.

Can we find $O(m+n)$ solution ? We have to reduce the search stage by at least one row or column in each iteration.

Initial SS of size : $m*n$

Final SS of size : 1

Total No. of step : $m+n$

How much to reduce SS by ? either m or n;

Now which cell allows us to reduce search space by m or n ? It must be

  • max in row , min in col
  • min in row , max in col

We can do a top-right or bottom-left search :

This approach make every search space a prefix submatrix of original matrix.

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    int n = matrix[0].size(),int m = matrix.size();
	int i = 0, j = n-1;
    while(i < m && j >= 0){
        if(matrix[i][j] == target) return true;
        
        // Ignore the column.
        if(matrix[i][j] < target)
            i++;
        else
           	j--;
    }
    return false;
}

Task Scheduler

There is greedy solution first take max frequency element which will give some idea of minimum cycles.

AAAABBBCCDE , n = 4

A _ _ A _ _ A _ _ A

Now we can fill smaller task on the gaps

A B _ A B _ A B _ A // this way they won’t wrap around :

A B C A B C A B D A

A B C E A B C A B D A // we can fill/create new slots in E if we want

Now say more than 1 task with max frequency

AAAA DDDD CCCC FFFEE , n = 3

ADCFEADCFEADCFADC

we see last DC are extra…

more e. g. AAAA DDDD CCCC F , n = 3

ADCFADCI ADCI ADC

I : idle we inserted !

max_count : Total number of task with max_freq

max_freq : frequency of the task which takes the most cycles.

gaps <- n

two cases

  • max_count - 1 >= gaps
  • max_count - 1 < gaps
int leastInterval(vector<char>& tasks, int n) {
    int m = tasks.size();
    vector<int> freq(26,0);
    int max_freq = 0, max_count;
    for(auto task : tasks){
        freq[task-'A']++;
        if(freq[task-'A'] == max_freq)
            max_count++;
        else if(freq[task-'A'] > max_freq){
            max_freq = freq[task - 'A'];
            max_count = 1;       
        }
    }
	// n gaps between two As
    if(max_count-1 >= n) return m;
    
    int count_processed = max_count * max_freq;
    int rem_count = m - count_processed;
    
    int total_gaps = (n - (max_count-1)) * (max_freq-1);
    
    if(total_gaps <= rem_count) return m;
    
    total_gaps -= rem_count;
    return m + total_gaps;
}